XiaoMi-AI文件搜索系统
World File Search System通过飞秒激光微加工引起的折射率剪裁的差异模式均衡
模式分割的多路复用技术与几种模式ERBIUM掺杂纤维放大器(FM-EDFA)相结合,显示出解决标准单模光纤(SSMF)传输系统的容量限制的重要潜力。但是,在FM-EDFA中产生的差异模式增益(DMG)从根本上限制了其传输能力和长度。在此,提出了使用飞秒激光微加工来调整折射率(RI)的创新DMG均衡策略。可变模式依赖性衰减可以根据FM-EDFA的DMG曲线来实现,从而实现DMG均衡。为了验证提出的策略,研究了常用FM-EDFA配置的DMG均衡。模拟结果表明,通过优化飞秒激光尾区域的长度和RI调节深度,在3个线性偏振(LP)模式组中,最大DMG(DMG MAX)在10 dB中降低了10 dB,而平均DMG(dmg ave)的平均dmg(dmg ave)。最后,实验证明了一个2-LP模式DMG均衡器,导致DMG最大最大从2.09 dB减少到0.46 dB,并且在C频带上将DMG AVE从1.64 dB降低到0.26 db,仅插入插入率为1.8 db。此外,使用5.4 dB实现了最大可变DMG均衡范围,满足了最常用的2-LP模式扩增方案的要求。
基于混合动态可计算一般均衡模型的可再生能源补贴削减对中国能源转型的影响
本文构建了一个混合可计算一般均衡模型,探讨了不同情景下减少可再生能源补贴对中国能源转型的影响。基准情景的结果表明,中国可以在2030年实现能源消费和结构以及碳排放强度的监管目标。本文设定了不同的政策情景来模拟2021年至2030年之间减少可再生能源补贴的影响。情景分析结果表明,政府2030年的能源和天然气消费总量以及碳排放强度目标可以实现。然而,在减少可再生能源补贴的情况下,非化石能源的目标很难实现。实证结果还表明,适度的可再生能源补贴加上可再生能源的重大技术进步是中国在2030年实现政府目标和能源转型的关键途径。
采用 MAS Blackboard 系统的 LiFePO4 电池储能系统的双层 SOC 和 SOH 均衡方案
1 齐齐哈尔大学机电工程学院,齐齐哈尔 161000;luzhongda@163.com;wangqilong3411@163.com;xufengxia_hit@163.com
基于弹性半空间理论的功率模块分布压装均衡热应力封装技术
基于弹性半空间理论的功率模块分布式压装均衡封装技术 常瑶,李成敏,IEEE 学生会员,罗浩泽,IEEE 会员,李武华,IEEE 会员,Francesco Iannuzzo,IEEE 高级会员,何翔宁,IEEE 研究员 摘要 – 本文研究了分布式压装(DPP)封装技术,以实现芯片的均衡热应力。在现有的集中压装(LPP)方式下,芯片上的机械应力分布本质上是不均匀的,并且与热应力分布相耦合,可以用弹性半空间理论模型来描述。通过分散集中压装载荷并均匀定位载荷,制定了夹紧阵列矩阵,并比较了不同夹紧方式下的机械应力分布。然后,选择了一种满足均衡应力分布和封装成本之间权衡的 3*3 夹紧方法。同时将汇流排与散热器集成在一起,提高功率模块的功率密度。最后,实现了DPP原型机,通过改变芯片周围的压力并对其进行加热,比较了原型机内部并联芯片之间的热分布,验证了所提出的基于弹性半空间理论的DPP封装技术对热应力平衡的影响。1
日本入境游客增加与农村经济的长期衰退:跨区域可计算一般均衡分析∗
摘要:入境旅游的增长有望刺激日本经济,因为游客的支出可以弥补由于人口减少而导致的消费下降。本研究使用多区域可计算一般均衡模型进行了模拟分析,以研究入境游客对日本 47 个县级地区的经济影响。由于入境游客访问所有地区,其经济在短期内增长。然而,对城市地区的影响更大,因为城市地区的游客数量多于农村地区。此外,从长远来看,人们从农村迁移到增长更快的城市地区,导致城市地区进一步增长和商业化。因此,即使旅游业导致整体经济增长,农村地区仍可能受到影响。为了发展农村地区,有必要专门吸引入境游客到这些地区。关键词:农村经济、经济衰退、入境游客、空间溢出效应、劳动力迁移、多区域 CGE JEL 代码:R12、Z32
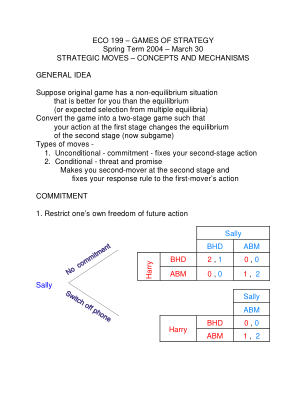
ECO 199 – 策略游戏 2004 年春季学期
假设原始博弈中存在非均衡情况,对你来说比均衡情况(或多个均衡中的预期选择)更好,将博弈转换为两阶段博弈,这样你在第一阶段的行动会改变第二阶段(现在是子博弈)的均衡,行动类型 - 1. 无条件 - 承诺 - 确定你的第二阶段行动,2. 有条件 - 威胁和承诺让你成为第二阶段的第二行动者,并将你的反应规则确定为第一行动者的动作
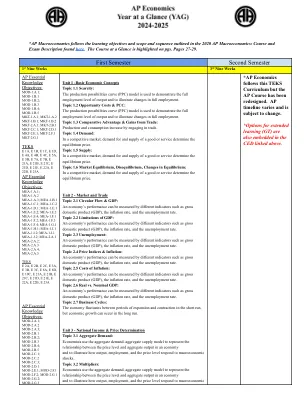
AP 经济学 YAG
第 1 单元 - 基本经济概念 主题 1.1 稀缺性:生产可能性曲线 (PPC) 模型用于展示产出的充分就业水平并说明充分就业的变化。 主题 1.2 机会成本和 PCC:生产可能性曲线 (PPC) 模型用于展示产出的充分就业水平并说明充分就业的变化。 主题 1.3 比较优势和贸易收益:通过从事贸易,生产和消费增加。 主题 1.4 需求:在竞争市场中,对商品或服务的需求和供应决定了均衡价格。 主题 1.5 供应:在竞争市场中,对商品或服务的需求和供应决定了均衡价格。 主题 1.6 市场均衡、不均衡、均衡变化:在竞争市场中,对商品或服务的需求和供应决定了均衡价格。
基于推理的一般和差分博弈策略调整
在许多多代理交互的环境中,每个代理的最佳选择在很大程度上取决于其他代理的选择。这些耦合的相互作用可以用一般和差分博弈很好地描述,其中玩家有不同的目标,状态在连续的时间中演变,最佳博弈可以用许多均衡概念之一来表征,例如纳什均衡。问题通常允许多重均衡。从这种博弈中的单个代理的角度来看,这种多重解决方案可能会带来其他代理行为方式的不确定性。本文提出了一个通用框架,通过推理其他代理所追求的均衡来解决均衡之间的歧义。我们在多人人机导航问题的模拟中演示了这个框架,得出两个主要结论:首先,通过推断人类所处的平衡状态,机器人能够更准确地预测轨迹;其次,通过发现并使自己适应这种平衡状态,机器人能够降低所有玩家的成本。
eco 199 b 策略游戏
选择 B 每个玩家优化自己的偏好(必须在内部逻辑上一致,但不必是纯粹自私的、金钱的或短期的) 均衡 B 选择之间的相互作用相互一致 战略思维过程的逻辑顶峰 完美计算的假设可能不切实际,并且可能无法达到均衡 但可以通过玩最有用的中心或焦点概念进行分析来学习计算和均衡
埃及气候行动概况中的公平能源转型
到2030年,新埃及将实现具有竞争力、均衡、多样化和知识型的经济,以公正、社会融合和参与为特征,拥有均衡和多样化的生态系统,受益于其战略位置和人力资本,实现可持续发展,让所有埃及人过上更好的生活