XiaoMi-AI文件搜索系统
World File Search System论计算短离散对数的量子算法中的后处理
摘要 我们重新审视了 Ekerå 和 Håstad 最近提出的用于计算短离散对数的量子算法。通过仔细分析该算法引起的概率分布,我们发现其成功概率高于以前报告的概率。受对分布理解的加深的启发,我们提出了一种改进的后处理算法,该算法比原始后处理算法效率更高、能够实现更好的权衡并且需要的运行次数更少。为了证明这些说法,我们通过对给定对数引起的概率分布进行采样,为该量子算法构建了一个经典模拟器。这个模拟器本身就是一项重要贡献。我们用它来证明,在针对具有短指数的 RSA 和 Diffie–Hellman 的加密相关实例时,Ekerå–Håstad 不仅在每次单独运行中,而且在整体上都比 Shor 更具优势。
中美贸易战的影响......
摘要 :中美贸易战影响了两国以及与其他国家的贸易。本研究调查了在贸易战阴影下,越南企业在 COVID-19 疫情期间的表现。我们用 2017 年至 2020 年越南对美出口对数的变化来衡量贸易战的影响,用中国对美出口对数的变化来衡量同期越南出口的变化。研究发现,贸易战影响较大的企业增加了投资、利润和附加值,这可能是由于非生产性企业退出市场。此外,贸易战对大企业的影响更为明显。外商投资企业从贸易战中获得的收益较少。疫情削弱了贸易战对企业业绩的影响,但却加剧了贸易紧张对外贸企业的影响。
减少量子因式分解中的量子比特数量
摘要本文重点研究了在 Z ∗ N 中因式分解和计算离散对数的量子算法中逻辑量子比特数量的优化。这些算法包含一个模 N 幂运算电路,它占了大部分成本,包括量子比特和运算成本。在本文中,我们表明,仅使用 o (log N ) 个工作量子比特,就可以获得模幂运算输出的最低有效位。我们将此结果与 May 和 Schlieper 的截断技术 (ToSC 2022) 以及 Shor 算法的 Eker˚aH˚astad 变体 (PQCrypto 2017) 相结合,仅使用 d + o (log N ) 个量子比特来解决 Z ∗ N 中的离散对数问题,其中 d 是对数的比特大小。因此,我们可以使用 n/2 + o(n) 个量子位来因式分解 n 位 RSA 模数,而当前设想的实现需要大约 2n 个量子位。我们的算法使用余数系统,并且以可参数化的概率成功。由于它是完全经典的,我们已经实现并测试了它。对于 RSA 因式分解,我们可以达到深度 O(n2log3n) 的门数 O(n3),然后必须将其乘以 O(logn)(Eker˚aH˚astad 所需的测量结果数)。要因式分解一个 RSA-2048 实例,我们估计 1730 个逻辑量子位和 236 个 Toffili 门就足以进行一次运行,而该算法平均需要 40 次运行。为了解决 2048 位安全素数组中 224 位(112 位经典安全性)的离散对数实例,我们估计 684 个逻辑量子位就足够了,并且每次使用 2 32 Toffili 门进行 20 次运行。
UAP 推进原理及飞行性能
二、推进系统的技术现状与问题 现阶段航天推进技术,唯一实用的推进系统是化学推进系统和电推进系统,它们都是基于质量的排出来引起动量推力。目前的推进系统广泛采用基于动量守恒定律的动量推力,由于其最大速度受气体有效排气速度与质量比的自然对数的乘积限制,其速度太慢,无法使飞船实现行星际旅行和恒星际旅行,因此一直亟待推进方式的突破。 2.1动量推力(反作用推力) 如上所述,目前除太阳帆和光帆外的各种推进系统都是基于动量守恒定律的。对于基于动量守恒定律的动量推力,其最大速度(V)受气体有效排气速度(w)与质量比的自然对数(R)的乘积限制。
1简介-Elliott Gordon Rodriguez
概率机器学习的最新进展已导致单纯形上的新分布家族。这种分布称为连续的分类,与Dirichlet具有相似之处,因为它定义了一个特别简单的封闭形式密度的指数族。然而,与Dirichlet(或任何基于对数的方法)不同,即使在零价值的组件存在下,连续的分类对数 - 样品函数也可以很好地定义,这使得此分布成为零元素组成数据的有效可能性模型,而无需归因于Zeros的插入。在此摘要中,我们回顾了我们的新颖分布的关键特性,并提出了一种应用,可以将其用于降低组成数据的尺寸。我们还突出了机器学习领域与组成数据分析之间的一些未置换的连接,我们的新颖分布密切相关。
来自细分的最佳几何局部量子和经典代码
几何局部量子码是一种位于 RD 内的纠错码,其中校验仅作用于固定空间距离内的量子位。主要问题是:几何局部代码的最佳维度和距离是多少?最近,Portnoy 在代码方面取得了重大突破,实现了高达多对数的最佳维度和距离。然而,这种构造调用了一个有点高级的数学结果,即将链复形提升到流形。本文绕过了这一步骤,并通过注意到一类良好的量子低密度奇偶校验码、平衡乘积码自然带有二维结构来简化构造。结合将在其他地方展示的新嵌入结果,这种量子码在所有维度上都实现了最佳维度和距离。此外,我们表明该代码具有最佳能量势垒。我们还讨论了经典代码的类似结果。
Authenticase M0689手册
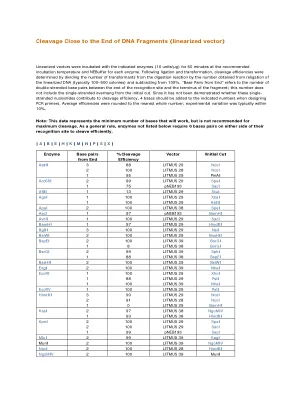
线性化载体与指定的酶(10单位/µg)在建议的孵化温度下60分钟,每种酶为星云孵育60分钟。在连接和转化后,通过将转化子与消化反应的数量除以从线性化DNA的宗教(通常为100-500个菌落)获得的数量来确定裂解效率,并从100%中减去。“从末端到基本对”是指识别位点末端和片段末端之间的双链基对数的数量;该数字不包括初始切割中的单链悬垂。由于尚未证明这些单链核苷酸是否有助于切割效率,因此在设计PCR引物时应将4个碱基添加到指定的数字中。平均效率被四舍五入到最接近的整数;实验变化通常在10%以内。
因果效应识别的最佳实验设计
Pearl's Do Colculus是一种从观察数据中学习可识别的因果关系效应的完整公理方法。当这种效果无法识别时,有必要在系统中执行通常昂贵的干预措施的集合来学习因果关系。在这项工作中,我们考虑了设计一系列干预措施的问题,并以最低成本确定所需的效果。首先,我们证明了此问题是NP完整的,随后提出了一种可以找到最佳解决方案或对数的算法的算法。这是通过在我们的问题与最小击球设置问题之间建立联系来完成的。此外,我们提出了几种多项式启发式算法来解决问题的计算复杂性。尽管这些算法可能会偶然发现亚最佳解决方案,但我们的模拟表明它们在随机图上产生了小的遗憾。