XiaoMi-AI文件搜索系统
World File Search System信函使用 VCII 实现线性电压控制正交振荡器
提出了一种基于新型 VCII 有源元件 [1, 2] 的线性电压控制正交振荡器 (LVCQO) 实现方法,该元件与现成的模拟乘法器设备 [3] 适当耦合。此处的设计拓扑利用模拟乘法器设备,通过其直流控制电压 kV(k ≡乘法常数 = 1/直流伏)[3] 方便地调整电路极点频率。文献表明,近期文献 [4-19] 中提出了具有电子可调特性的此类振荡器设计,如表 I 所示;其中只有少数表现出线性可调特性。先前此类拓扑中的设计使用某些设备偏置电流 (I b ) 或设备跨导参数 (gm ) 或被动调谐 [20];因此,设计需要额外的电流处理电路,这会引起热 (VT ) 和静态耗散问题。提出的振荡器设计实现方法利用一对新型 VCII,它们由一对模拟乘法器适当调谐
基于电压可变电感器的线性电压控制正交振荡器实现
Ź i = Zi/ α 1 β 1 α 2 δ 2 (2) 其中 α 1,2 = (1 ─ε i,1,2 )/ (sτ i,1,2 +1) ,β 1 = (1 ─ε v1 )/ (sτ v1 +1) 和 δ 2 = (1 ─ε o1 )/ (sτ o1 +1)。直流增益误差完全可以忽略不计 ( ε << 1)[ 13] ;滚降极点出现在非常高的频率范围 (>> 100MHz) 并且它们非常接近 [14 ]。因此,我们可以写出 τ i,v,z ≈τ ≡ 1/ω p ,从而得出 α 1 β 1 α 2 δ 2 = 1/ { (sτ) 4 + (4sτ ) 3 + (6sτ) 2 + 4s τ +1 (3)忽略高阶项,对于频域写出 sτ = jωτ ≡ jω/ω p ≈ ju ;我们得到一个修正的 L 值,其中 u << 1,因为 Ĺ /L ≈ {1/ √(1+16 u 2 )} ∟─arctan (4 u ); u << 1 (4)因此,器件滚降极点的影响可以忽略不计。如图 1(a) 所示,将所提出的 VVI 应用于具有分流电容器 (C s ) 和串联电阻器 (r) 的选择性 BP 滤波器中,其传递函数为 V o /V i (s) ≡ F(s) 为 F(s) = (sL/r)/ { s 2 LC s (1+ m ) +(sL/r) + 1} (5)
在微波振荡器中诱导高角度动量自旋动力学
如何修复?1)多数投票错误校正:在三个位置进行冗余的存储位,定期检查所有三个位置 - 如果一个人翻转 - 基于多数投票重置三个物理位的组合= 1'逻辑'位
量子参量振荡器中共振力引起的对称性破缺
参量振子的量子动力学越来越受到理论和实验界的关注 [1-16]。在一定程度上,这种兴趣来自于参量振子的新应用,特别是在量子信息领域的应用。在更广泛的背景下,此类振子为研究远离热平衡的量子动力学和揭示其迄今未知的方面提供了一个多功能平台,隧穿新特征和新的集体现象就是例子。动力学特征之一是多态量子系统中详细平衡的出现和特征,这也是本文的动机之一。在很大程度上,参量振子的重要性在于其对称性。此类振子是具有周期性调制参数(如特征频率)的振动系统,其振动频率为调制频率 ω p 的一半。经典上,振动态具有相等的振幅和相反的相位 [17],这是周期倍增的一个基本例子。量子力学上,振动态可被认为是符号相反的广义相干态 [18]。弗洛凯本征态是频率为 ω p / 2 的振动态的对称和反对称组合。一般来说,在量子信息中使用参量振子需要进行破坏其对称性的操作,参见文献 [19]。对称性破坏可以通过在频率为 ω p / 2 处施加额外的力来实现。从经典角度来看,这种力的作用可以从图 1(a) 中理解。由于振动态具有相反的相位,因此力可以与两个状态中的其中一个同相,从而增加其
第四届天体物理和实验室等离子体原子光谱和振荡器强度国际研讨会
座谈会这是 1983 年在瑞典隆德大学举行的一系列座谈会中的第四次,随后在俄亥俄州托莱多和荷兰阿姆斯特丹举行。这些会议的目的是为原子光谱数据的主要用户和这些数据的提供者提供一个国际交流论坛。这为用户提供了一个机会来审查他们现在和未来的需求,也为提供者提供了一个机会来审查他们的实验室能力、数据测量的新发展以及改进
量子层析成像中的量子层析成像中的三阶集成光学参数振荡器
简介。新型的光子量子技术依赖于非经典光的集成来源,从而产生了从单光子到明亮场的纠缠状态的范围。光学参数振荡器(OPO)被广泛用于此目的。纳米光子学的发展将这些设备带入了微观领域[1]。如今,它们代表了纠缠光子的可靠来源[2],是实现综合信息信息协议的基础[3]。在连续变量域中,实现了几个重要的里程碑,例如使用第二(χ(2))[4,5]和三阶(χ(3))非线性[6-11]的片上光学挤压。尤其是硅光子学引起了人们的极大兴趣,因为它们与CMOS(互补的金属 - 氧化物 - 氧化型)制造过程的兼容性,从而使光子和微电源在同一芯片中无缝整合。由其成熟的制造业杠杆作用,低损失波导是局部制造的,导致超高质量因子光学微型洞穴[12]。在这里,我们首次介绍了在片上OPO中产生的完整高斯州的完整量子断层扫描。是针对这些系统中纠缠的观察,在参考文献中进行了理论预测。[13,14],我们使用谐振辅助
课程概要描述
交流信号源 - 振荡器 - 振荡器的选择 - 巴克豪森标准。音频振荡器(维恩电桥振荡器 - 相移振荡器) - 射频振荡器(考毕兹振荡器 - 哈特利振荡器) - 晶体振荡器。信号发生器 - 扫频发生器 - 脉冲和方波发生器 - 函数发生器 - 衰减器。谐波分析 - 波形频谱 - 使用傅立叶变换器的谐波失真分析。谐波分析仪器 - 谐波失真分析仪。波形分析仪 - 频谱分析仪。传感器 - 传感器的分类 - 传感器的选择 - 应变传感器 - 位移传感器 - 电容式传感器 - 电感式传感器 - 压电传感器 - 温度传感器 - 光电传感器。数据采集系统 - 信号调理电路 - 数模转换器和模数转换器。数据采集系统和计算机控制测量。
使用CMOS逆变器和差分对放大器作为延迟元素的环振荡器配置的比较分析
摘要 - 环振荡器是集成电路的必要块,充当数字时钟生成器。该振荡器有几种进度技术。然而,最适当的环振荡器的拓扑选择需要对电气特征进行权衡的分析。本文介绍了两个拓扑之间的比较研究,以实施环振荡器。每个拓扑都使用特定的延迟单元格:CMOS逆变器或差分对放大器。目标输出频率为10.44 MHz,振荡器以130 nm的技术实现。拓扑是根据功率耗散,硅面积和制造过程变化的比较。电气模拟表明,逆变器环振荡器具有较小的功耗和较小的硅面积。在另一侧,差分放大器振荡器对过程变化的敏感性较小。这些结果可以帮助指导设计师确定适合集成电路设计中系统要求的最佳拓扑。索引项 - 逆变器,差分对,环振荡器,人体动作过程变化。
45 nm CMOS中的环振荡器和电流饥饿VCO的比较和性能分析
因此,随着时钟速度的增加,需要更加间隔的多相时钟。常规的CMOS环振荡器已被普遍用于这些应用程序,因为它们由于高速操作和简单的结构而可以提供多相时钟信号。在常规环振荡器中,振荡频率取决于单个延迟之和的两倍的倒数。此外,传统环振荡器中的最小龙头间距不能小于两个逆变器延迟。在这里,我们必须添加更多的逆变器才能获得更多的输出阶段,从而降低了最大工作频率。要获得一个较小的间距,由一系列耦合环振荡器组成的阵列振荡器,可以将延迟分辨率延迟到逆变器延迟,从而提出了将逆变器延迟除以除以环的数量。因为该电路基于阵列结构,但是,多相输出的数量仅限于环中阶段的倍数。
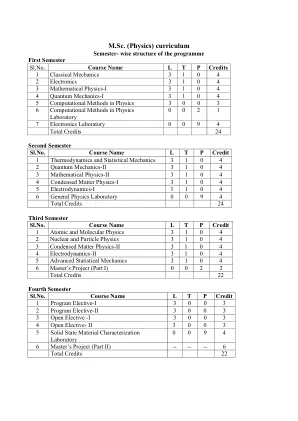
理学硕士(物理学)课程
第一单元电子设备(10 L)先进电子设备:半导体肖特基二极管简介、半导体二极管、齐纳二极管、隧道二极管及其应用、双极型晶体管及其操作和特性、偏置和稳定、晶体管混合模型、使用 h 参数分析晶体管放大器电路、结型场效应晶体管的特性、JFET 的偏置、金属氧化物半导体 JFET 的概念和应用、光电二极管、发光二极管和太阳能电池、电源(包括整流和滤波电路)和调节器。第 2 单元反馈放大器和振荡器(8 L)放大器的分类、反馈的概念、负反馈和正反馈的一般特性、振荡器原理、巴克豪森标准、科尔皮特和哈特利振荡器、RC 振荡器、温桥振荡器、RC 相移振荡器、多谐振荡器、非稳态、单稳态和双稳态多谐振荡器、方波、三角波发生器和脉冲发生器