XiaoMi-AI文件搜索系统
World File Search System极限的
通过纳米多孔石墨烯膜的致密液体传输，处于空间排除的极限
我们研究了使用分子动力学（MD）和有限元仿真的空间排除极限的密集流体通过纳米多孔膜的运输。仿真结果表明，对于简单的流体，桑普森流的偏差是滑动和有限原子尺寸效应之间竞争的结果。后者通过引入有效的孔径以及有效的膜厚度来表现出来。我们提出了一个解释所有这些因素的膜渗透性的分析模型。我们还展示了如何修改该模型以描述低分子量芳族烃在空间极限下跨这些膜的转运。通过Lennard-Jones流体渗透到单层和多层石墨烯膜的Lennard-Jones流体以及低分子量有机液体渗透到单层石墨烯膜的MD模拟进行了广泛的验证。
3D 打印介电晶体的有效介电常数测量
摘要 — 增材制造为创新天线和微波元件提供了新的可能性。为了充分发挥其潜力，必须充分利用 3D 打印技术提供的功能。3D 打印结构化电介质目前在这方面受到广泛关注。然而，表征这种晶体结构的介电性能并不容易，而且经常需要对这种性能做出假设。本文展示了在具有不同填充率的简单立方 (SC) 和面心立方 (FCC) 晶体几何中，增材制造结构化电介质的介电常数和损耗角正切的表征。将测量结果与 Maxwell-Garnett 有效介质近似预测的值以及从长波长极限的三维平面波展开法 (PWEM) 中提取的有效折射率进行了比较。
二九百万个固有的Q-因子整体化...
最近的薄膜锂锂（TFLN）的出现扩展了综合光子学的景观。这是通过TFLN晶圆的商业化和TFLN的高级纳米化来实现的，例如高质量的干蚀刻。但是，制造缺陷仍然将传播损失限制为几个dB/m，严格严格该平台的影响。在这里，我们证明了具有创纪录的内在质量（Q）系数的TFLN微孔子，为2900万，对应于1.3 dB/m的超低传播损失。我们提出了频谱分析和Q因子跨不同谐振几何形状的统计分布。我们的工作推动了TFLN光子学的制造极限，以在材料极限的1个数量级内实现Q因子。©2024中国激光出版社
HD8 e5-8x4-1.ai - 阿斯特拉依维柯
由具有高弹性极限的特种钢制成，由两个平行的扁平侧梁（宽度 820 毫米）组成，C 型截面（320x90x10 毫米），通过钉子横梁连接在一起 RBM（轨道弯曲力矩）：202,020 Nm（20,593 Kgm）。钢制前保险杠，带大灯保护格栅、前部机动钩、后部防钻杆、前踏板、第二轴橡胶挡泥板、300 升钢制油箱。按需提供：用于轮胎充气的快速释放压缩空气连接。后防钻护板处于缩回位置。混凝土搅拌机的超长底部防护杆。后部机动钩。自动后拖钩。第三和第四轴上有橡胶挡泥板。备胎侧绞盘（轴距 2350 - 2600 - 2850 除外）
瓦朗加尔国立科技学院
PO1 PO2 PO3 PO4 PO5 PO6 CO1 3 3 2 2 2 3 CO2 3 2 2 3 3 2 CO3 3 2 3 3 2 3 CO4 3 3 3 3 2 3 教学大纲： 基础拓扑：简介 黎曼斯蒂尔杰积分：积分的定义和存在性，积分的性质，具有可变极限的积分的积分和微分。 不正确积分：定义及其收敛性，收敛测试， 和 函数。 一致收敛：一致收敛的测试，和函数的极限和连续性定理，函数级数的逐项微分和积分。 幂级数：收敛及其性质。 傅里叶级数：狄利克雷条件、存在性、问题、半程正弦和余弦级数。学习资源：教科书：1. 数学分析原理，Walter Rudin，McGraw Hill，2017，第三版。2. 实分析，Brian S.Thomson，Andrew M.Bruckner，Judith B.Bruner，Prentice Hall
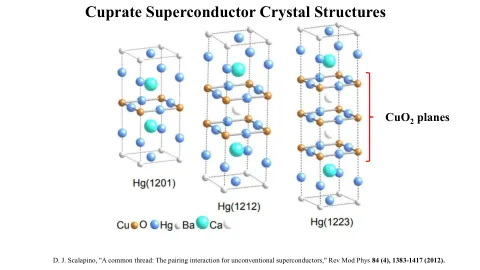
库酸盐超导体晶体结构
还表明，对通过测量超导状态的骑士移位，对旋转单线态。电子自旋和核矩之间的相互作用是ℋ=⃗𝑖𝑖𝑖𝑖𝑖𝑖𝐼𝐼⃗𝐼𝐼⃗𝐼𝐼𝐼𝐼，导致骑士移位𝐾𝐾（𝑇𝑇），可测量电子自旋易感性。这观察到在零温度极限的零，与自旋单重配对状态一致。[M. Takigawa，A。P. Reyes，P。C. Hammel，J。D. Thompson，R。H. Heffner，Z。Fisk，Z。Fisk和K. C. Ott，“ YBA 2 CU 3 O 6.63（T C = 63 K）的磁性特性的CU和O NMR研究，” Phys Rev B 43（1），247-257（1991）
量化开放量子动力学中的非马尔可夫性
非马尔可夫开放量子动力学的表征具有理论和实践意义。在一篇开创性的作品 [ Phys. Rev. Lett. 120, 040405 (2018) ] 中，提出了一个必要且充分的量子马尔可夫条件，具有清晰的操作解释和与经典极限的对应关系。在这里，我们为一般开放量子动力学提出了两个非马尔可夫性测度，它们与马尔可夫极限完全相一致，并且可以基于系统的多时间量子测量进行有效计算。提出了一种重建底层开放量子动力学的启发式算法，其复杂性与提出的非马尔可夫性测度直接相关。通过数值示例展示了非马尔可夫性测度和重建算法，并仔细重新审视了量子失相动力学中的非马尔可夫性。
协变量子纠错的新视角
协变码是一种量子码，逻辑系统上的对称变换可以通过物理系统上的对称变换来实现，通常具有有限的量子纠错能力（一个重要的例子是 Eastin-Knill 定理）。理解协变量子纠错极限的需求出现在物理学的各个领域，包括容错量子计算、凝聚态物理和量子引力。在这里，我们从量子计量和量子资源理论的角度探索了连续对称性的协变量子纠错，在这些以前分散的领域之间建立了牢固的联系。我们证明了协变量子纠错不保真度的新的、强大的下界，这不仅扩展了以前不行的结果的范围，而且比现有界限有了很大的改进。为擦除和去极化噪声推导出了明确的下界。我们还提出了一种几乎饱和这些下界的协变码。