XiaoMi-AI文件搜索系统
World File Search System快速反演,预条件量子线性系统......
在经典迭代线性系统求解器中,预处理是处理病态线性系统最广泛和最有效的方法。我们引入了一种称为快速求逆的量子原语,可用作求解量子线性系统的预处理器。快速求逆的关键思想是通过量子电路直接对矩阵求逆进行块编码,该电路通过经典算法实现特征值的求逆。我们展示了预处理线性系统求解器在计算量子多体系统的单粒子格林函数中的应用,该函数广泛用于量子物理、化学和材料科学。我们分析了三种情况下的复杂性:哈伯德模型、平面波对偶基中的量子多体哈密顿量和施温格模型。我们还提供了一种在固定粒子流形内进行二次量化格林函数计算的方法,并指出这种方法可能对更广泛的模拟有价值。除了求解线性系统之外,快速求逆还使我们能够开发用于计算矩阵函数的快速算法,例如高效准备吉布斯态。我们分别基于轮廓积分公式和逆变换介绍了两种高效的此类任务方法。
系统辨识中一般矩阵的量子线性系统算法
摘要:求解线性方程组是经典辨识系统中最常见、最基本的问题之一。给定一个系数矩阵A和一个向量b,最终任务是寻找解x使得Ax=b。基于奇异值估计技术,该文提出一种改进的量子方案,对于一般的m×n维矩阵A,在O(κ2√rpolylog(mn)/ϵ)时间内得到线性方程组解对应的量子态|x⟩,该方案优于现有的量子算法,其中κ为条件数,r为矩阵A的秩,ϵ为精度参数。同时,我们还设计了一个针对齐次线性方程组的量子电路,并取得了指数级的提升。我们方案中的系数矩阵A是与稀疏性无关的非方阵,可以应用于更一般的场合。我们的研究提供了一个通用的量子线性系统求解器,可以丰富量子计算的研究范围。
TILT:在囚禁离子线性系统上实现更高的保真度......
摘要 — 离子阱量子比特是实用量子计算的领先技术。在这项工作中,我们对离子阱的线性磁带架构进行了架构分析。为了实现我们的研究,我们开发并评估了该架构的映射和调度算法。特别是,我们引入了 TILT,这是一种线性“图灵机式”架构,具有多激光控制“头”,其中线性离子链在激光头下来回移动。我们发现,与同等大小的量子电荷耦合器件 (QCCD) 架构相比,TILT 可以大大减少通信。我们还为 TILT 开发了两种重要的调度启发式方法。第一个启发式方法通过将沿相反方向传输的数据匹配为“反向交换”来减少交换操作的数量,并且还避免了跨头部宽度的最大交换距离,因为最大交换距离使得在一个头部位置调度多次交换变得困难。第二种启发式方法通过将磁带调度到每次移动时可执行操作最多的位置来最小化离子链运动。我们从模拟中提供了应用程序性能结果,这表明 TILT 在一系列 NISQ 应用程序中的成功率可以胜过 QCCD(平均高达 4.35 倍和 1.95 倍)。我们还讨论了使用 TILT 作为构建块来扩展现有的可扩展离子阱量子计算方案。索引术语 — 量子计算、离子阱架构、电路优化
线性系统 L2 稳定的输出反馈律和事件触发条件的共同设计
我们研究了使用输出反馈事件触发控制器的线性系统的 L 2 稳定性。特别是,我们感兴趣的场景是,工厂输出和控制输入分别通过两个不同的数字通道传输到控制器和执行器,这两个数字通道有自己的采样规则。工厂动态受外部干扰的影响,输出测量和控制输入受噪声干扰。我们提出了一种协同设计程序,用于同时合成动态输出反馈定律和事件触发条件,使得闭环系统在 L 2 增益上界给定的情况下是 L 2 稳定的。所需条件以线性矩阵不等式 (LMI) 的可行性来表述。然后,我们利用这些 LMI 来最大化工厂输出和/或控制输入两次传输之间的保证最短时间。我们还提出了一种启发式方法来减少每个通道的传输量。所开发的技术将时间驱动(因此是周期性的)采样作为特殊情况,并且结果在此背景下也是新颖的。所提出方法的有效性通过数值示例得到说明。
关于求解条件数中运行时间二次改进的正定量子线性系统类
用于解决量子线性系统 (QLS) 问题的量子算法是近年来研究最多的量子算法之一,其潜在应用包括解决计算上难以解决的微分方程和提高机器学习的速度。决定 QLS 求解器效率的一个基本参数是 κ,即系数矩阵 A 的条件数,因为自从 QLS 问题诞生以来,我们就知道,在最坏情况下,运行时间至少与 κ 呈线性关系 [1]。然而,对于正定矩阵的情况,经典算法可以求解线性系统,运行时间扩展为 √κ,与不确定的情况相比,这是一个二次改进。因此,很自然地会问 QLS 求解器是否可以获得类似的改进。在本文中,我们给出了否定的答案,表明当 A 为正定时,求解 QLS 也需要与 κ 呈线性关系的运行时间。然后,我们确定了可以规避此下限的正定 QLS 的广泛类别,并提出了两种新的量子算法,其特点是 κ 的二次加速:第一种基于有效实现 A − 1 的矩阵块编码,第二种构建形式为 A = LL † 的分解来预处理系统。这些方法适用范围广泛,并且都允许有效地解决 BQP 完全问题。
MATH435教学大纲,第241项(2024年秋季) - 数学
课程描述:一阶标量微分方程。初始价值问题。存在,独特性,对初始数据的持续依赖。线性系统具有恒定系数。 指数矩阵。 线性和几乎线性系统的渐近行为。 二维自主系统。 关键点及其分类。 相平面分析。 Lyapunov稳定理论的简介。线性系统具有恒定系数。指数矩阵。线性和几乎线性系统的渐近行为。二维自主系统。关键点及其分类。相平面分析。Lyapunov稳定理论的简介。
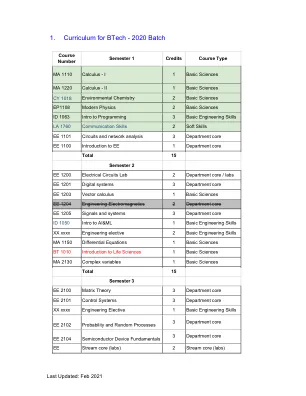
1。BTECH的课程-2020 Batch
这些课程与EE课程中的核心课程具有显着的重叠(> 60%)。因此,普通的EE学生不应根据任何“选修”类型选择他们。但是,允许替换后的BTECH电气工程和分支更换器进入EE。这有助于改变分支机构,以迅速赶上第一学期的错过课程。1。EE1101电路和网络分析可以用EE1102-BASIC电气工程取代2。 EE1201数字系统可以用EE1202数字电路代替3。 EE1205信号和系统可以用EE1206线性系统和信号处理代替。 4。 EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE1101电路和网络分析可以用EE1102-BASIC电气工程取代2。EE1201数字系统可以用EE1202数字电路代替3。 EE1205信号和系统可以用EE1206线性系统和信号处理代替。 4。 EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE1201数字系统可以用EE1202数字电路代替3。EE1205信号和系统可以用EE1206线性系统和信号处理代替。 4。 EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE1205信号和系统可以用EE1206线性系统和信号处理代替。4。EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。3。a)不允许的课程列表,因为EE BTECH学生的部门选修课
量子数值线性代数简介
▶ 因式分解 ▶ 非结构化搜索 ▶ 离散傅里叶变换 ▶ 应用数学:线性系统,微分方程,最优化,机器学习,· · · 量子算法动物园:https://quantumalgorithmzoo.org 林林的讲义:[arXiv:2201.08309]