XiaoMi-AI文件搜索系统
World File Search System随机变量
随机变量的期望值与标准差
我们感兴趣的问题不仅是关于随机变量的分布或其概率，而且我们可能想要确定随机变量的“平均值”或期望值，以及它与其期望值或标准差的偏差程度。我们将只研究离散随机变量的期望值和标准差，这些离散随机变量是其可能值集合形成可数不同值列表的随机变量。例如，博兹曼医院接下来的三胎女孩数量就是一个离散随机变量，因为它只能取值 0、1、2 或 3。离散随机变量可以取无限数量的可能值，只要我们能够将它们列在有序列表中。例如，掷硬币直到第一次出现正面的次数是一个离散随机变量，可能值为 1、2、3、4、...可以在某个间隔内取任意值的随机变量（例如时间、长度、利率、高度）称为连续随机变量。我们将使用以下符号来指定离散随机变量可能结果的概率：
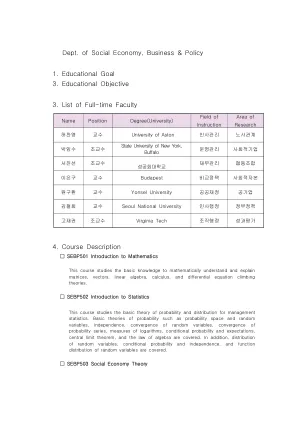
社会经济、商业与政策系
统计学。涵盖概率空间和随机变量、独立性、随机变量的收敛性、概率级数的收敛性、对数测度、条件概率和期望、中心极限定理和代数定律等概率的高级理论。此外，还涵盖随机变量的分布、条件概率和独立性以及随机变量的函数分布。
标准化互信息估计
统计学中一个非常重要的问题是两个随机变量之间的依赖程度，或者一个随机变量包含的关于另一个随机变量的信息量。互信息给出了这个问题的答案，但它肯定可以得到改进。互信息总是非负的，但它没有统一的上限。这使得仅基于互信息来解释两个随机变量的关联强度变得困难。这引出了一个问题：互信息必须有多大，才能认为两个随机变量相互依赖，甚至完全依赖？在本文中，我们将通过定义一个标准化的互信息 κ 来考虑这个问题的一个可能的解决方案，该 κ 具有严格介于零和一之间的优点。当且仅当两个随机变量独立时，这个 κ 才具有等于零的理想特性，当且仅当两个随机变量具有一一对应关系时，它才等于一。我们还将考虑 κ 的估计以及我们开发的估计量的渐近性质。
可靠性工程.pdf
为了将概率论应用于可靠性评估，研究系统行为，必须进行一系列实验或推导出数据收集方案。为了将概率论应用于这些随机值或事件的发生，我们需要研究这些称为随机变量的变量。∴ 随机变量是一个变量，表示给定随机实验的结果或成果。随机变量是只能具有离散状态数或可数值的变量。随机变量可以是“离散的”或“连续的”。离散随机变量是只能具有离散状态数或可数值的变量。例如：1. 抛硬币 - 结果是正面或反面。2.掷骰子 - 结果是 1、2、3、4、5 或 6。连续随机变量是取无限多个值的变量，或者其范围形成一组连续的实数。这并不意味着范围从 - ∞ 延伸到 + ∞。它只意味着值有无数种可能性。例如：1.灯泡的使用寿命。2.如果电流的值在 5A 和 10A 之间，则表示连续随机变量。概率密度函数 与随机变量相关的概率可以用称为概率密度函数或概率质量函数的公式来描述。我们使用符号 f(x) 表示概率密度函数。
![arXiv:2412.15800v1 [quant-ph] 2024 年 12 月 20 日](/simg/g:\will\search\icon\source\6\6aa1457dbabd38ca90a7863ebeb46fbce8984a72.webp)
arXiv:2412.15800v1 [quant-ph] 2024 年 12 月 20 日
众所周知，密度矩阵并不总能区分不同的量子计算误差（参见 [9]）。因此，用随机变量表示量子计算误差比用密度矩阵表示更准确。这就是我们决定用随机变量来表示量子计算误差的主要原因。而且，一旦用随机变量建立了量子计算误差的表示，那么衡量量子计算误差大小的最自然参数就是方差。随机变量 X 的方差定义为 X 的平均值 µ 的二次偏差的平均值，V ( X ) = E [ ∥ X − µ ∥ 2 ]。在我们的例子中，由于随机变量 X 表示量子计算误差，因此 X 的平均值是无误差计算得到的 n − 量子比特 Ψ 0 。不失一般性，我们假设所有量子计算误差的平均值始终为 Ψ 0 = | 0 ⟩ 。为此，只需通过幺正变换将 Ψ 0 移到 | 0 ⟩ 即可。因此，使用公式 (1) 给出的纯量子态，X 的方差将为：
课程和教学大纲
线性方程的线性代数系统：矩阵的范围空间和空空间，矩阵的等级，线性方程系统的解决方案的存在和唯一性，与线性方程系统相关的解决方案空间的尺寸。向量空间：向量空间，子空间，双空间，内核，空空间，线性独立性和依赖性，线性跨度，基础，维度，直接总和，线性变换。矩阵表示：特征值和特征向量，相似性，等级和无效，对角线化，约旦形式。随机变量和随机过程随机变量，分布和密度函数，力矩和力矩生成功能，多元分布，独立的随机变量，边际和条件分布，条件期望，随机变量的转换，随机变量的转换，随机过程的元素，随机过程的元素，一般随机过程的分类。马尔可夫链：定义，示例，过渡概率，状态和链的分类，基本限制定理，限制马尔可夫链的分布。ODE的ODE和计算系统的系统：通过Lipchitz条件，解决方案和稳定性的解决方案的存在和独特性。变化的计算：变分问题的示例，变异问题的基本计算，弱和强大的极端和强大的终点问题，哈密顿量。参考：
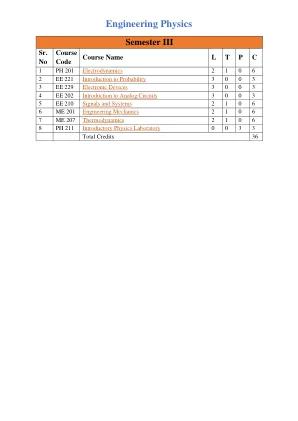
工程物理学
简介：学习本课程的动机、必修基础数学复习、实线子集上概率与长度的关系、概率形式定义、事件与$\sigma$代数、事件独立性与条件概率、事件序列与Borel-Cantell引理。随机变量：随机变量的定义、随机变量的类型、CDF、PDF及其性质、随机向量与独立性、随机变量变换简介、高斯随机向量简介。数学期望：通过例子了解平均值的重要性、期望的定义、矩与条件期望、MGF、PGF与特征函数的使用、方差与k阶矩、MMSE估计。不等式与收敛概念：马尔可夫、切比雪夫、切尔诺夫与Mcdiarmid不等式、概率收敛、均值与几乎必然、大数定律与中心极限定理。随机过程的简要介绍：示例和正式定义、平稳性、自相关和互相关函数、遍历性的定义。
B.Tech Power电子和仪器
模块1：线性代数简介（8个讲座）向量，向量空间，线性独立性，碱基和维度，正交性，线性图和矩阵，矩阵的基本子空间，rank-nullity Theorem。模块2：光谱分解（6个讲座）特征值，不变子空间，内部产物，规范，正统碱基，光谱定理，等法，极值和奇异值分解，应用。模块3：矩阵（5个讲座）特殊矩阵，规范和决定因素的特性。模块4：概率简介（6个讲座）经典和公理概率，概率空间，条件概率和独立性，总概率，贝叶斯规则。模块5：随机变量（8个讲座）定义，常见示例，累积分布函数，概率质量函数，概率密度函数；随机变量的函数；期望 - 卑鄙，差异和时刻；特征和瞬间的功能；特殊的随机变量 - 二项式，泊松，统一，指数和高斯；共同时刻，有条件的期望；协方差和相关性 - 独立，不相关和正交随机变量；两个随机变量的函数；大量法律和中央限制定理的法律薄弱。模块6：随机过程简介（3个讲座）离散和连续时间过程；随机过程的概率结构；卑鄙，自相关和自相关功能；随机过程的示例：白噪声。文本/参考书：
讲座5：无监督的学习
p（a | b;α）给定b的概率，由α参数化。注意：α是模型的参数，而不是随机变量x〜Bernoulli（p）x是带有参数p的Bernoulli随机变量。思考：x表示硬币折腾的结果，p（h）= p x〜多项式（φ）x是一个多项式随机变量，具有参数φ和n = 1-这是Bernoulli随机变量的概括。思考：x表示滚动骰子的结果，p（side-i）= p（i）; φ= {p（1），。。。，p（6）} z一个随机变量，以指示滚动k flace die的结果（k = 2：bernoulli;多项式;否则）p（z（j）= i）从高斯i绘制数据点的概率。这更多是一种信念或先验，并且独立于数据。思考：上帝将其设置为先验p（z（j）= i | x（j））X（j）点是从高斯 - i生成的概率，因为我们观察到x（j）。将其视为：我们观察到x（j），现在是从高斯i绘制的吗？p（x（j）| z（j）= i）观察x（j）的概率，因为我们正在从z（j）= i生成数据;在本讲座中，我们假设x（j）| z（j）= i〜n（µ（i），σ（i））θθ一组模型参数；如果k = 2，θ= {µ（1），µ（2），σ（1），σ（2），p}