机构名称：
¥ 1.0
p（a | b;α）给定b的概率，由α参数化。注意：α是模型的参数，而不是随机变量x〜Bernoulli（p）x是带有参数p的Bernoulli随机变量。思考：x表示硬币折腾的结果，p（h）= p x〜多项式（φ）x是一个多项式随机变量，具有参数φ和n = 1-这是Bernoulli随机变量的概括。思考：x表示滚动骰子的结果，p（side-i）= p（i）; φ= {p（1），。。。，p（6）} z一个随机变量，以指示滚动k flace die的结果（k = 2：bernoulli;多项式;否则）p（z（j）= i）从高斯i绘制数据点的概率。这更多是一种信念或先验，并且独立于数据。思考：上帝将其设置为先验p（z（j）= i | x（j））X（j）点是从高斯 - i生成的概率，因为我们观察到x（j）。将其视为：我们观察到x（j），现在是从高斯i绘制的吗？p（x（j）| z（j）= i）观察x（j）的概率，因为我们正在从z（j）= i生成数据;在本讲座中，我们假设x（j）| z（j）= i〜n（µ（i），σ（i））θθ一组模型参数；如果k = 2，θ= {µ（1），µ（2），σ（1），σ（2），p}
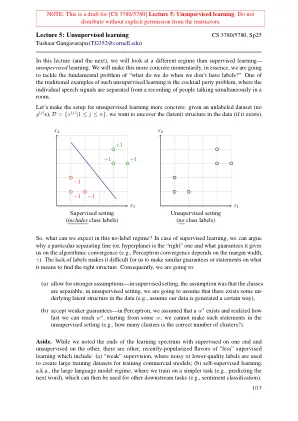
讲座5：无监督的学习
主要关键词
相关文件推荐
