XiaoMi-AI文件搜索系统
World File Search System开放量子系统理论简介
本稿是 2022 年春季/夏季波兰科学院物理研究所博士学校开设的一学期研究生课程讲义的编辑和完善版本。本课程仅要求学生具备研究生水平的量子力学基础知识。讲义本身基本上是自成体系的,可以用作开放量子系统主题的教科书。本课程的计划基于一种描述开放系统动力学的新方法:展示了如何用多组分准随机过程来表示与系统耦合的环境自由度。使用这种表示,可以构建系统动态图的超准累积量(或超量子量)展开——这种参数化自然有助于开发稳健且实用的扰动理论。因此,即使是经验丰富的研究人员也可能会发现这份手稿很有趣。
双学位(电气工程学士学位 + 硕士学位)
28/29 第三学期 广度 – 1 3-0-0 3 3 电子学概论 EC2L001 3-1-0 4 4 材料科学与工程概论 ID2L001 2-0-0 2 2 生物科学与技术概论 ID2L002 2-0-0 2 2 概率统计与随机过程 MA2L003 3-1-0 4 4 信号与系统 EC2L002 3-1-0 4 4 电子学概论实验室 EC2P001 0-0-3 2 3 信号与系统实验室 EC2P002 0-0-3 2 3 研讨会 EE2S001 0-0-3 2 3 总计 25 28 第四学期 横向 -1 3-0-0/3-1-0 3/4 3/4 广度 – 2 3-0-0/3-1-0 3/4 3/4 环境科学技术与管理 ID2L003 2-0-0 2 2 网络理论 EE2L001 3-0-0 3 3 电机 EE2L003 3-1-0 4 4 数字电子与微处理器 EC2L006 3-1-0 4 4 电机实验室 EE2P003 0-0-3 2 3 数字电子与微处理器实验室 EC2P006 0-0-3 2 3 总计 23/25 25/27
关联 HALT 和 HASS、RS/HALT 振动和最终用途...
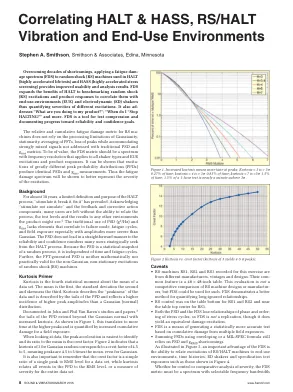
背景 近 30 年来,HALT 过程的定义和目的一直很有限,即“刺激、破坏、修复”。由于承认“刺激而非模拟”以及反馈和纠正措施组件,许多用户无法将过程、测试水平和结果与产品可能遇到的任何其他环境联系起来。5 PSD (g 2 /Hz) 和 g rms 的传统用法缺少与故障模式、疲劳循环和现场暴露相关的元素,尤其是振幅比高斯更严重的情况下。PSD 不能直接导致许多用户从 HALT 过程中战略性地寻求的可靠性和置信度数字。由于 PSD 是随机过程的统计快照,因此它与时间和疲劳循环无关。此外,对于随机冲击 (RS) 机器的非高斯、非平稳激励,FFT 生成的 PSD 在数学上和实践上都无效。
数字PCR - Qiacuity One 5plex
保险公司必须准确衡量风险才能设定保费,银行必须了解其在金融市场中发生冲击的风险,并且公共当局在确定规划法规时必须估算洪水和其他灾难的可能规模。准确的风险估计涉及从观察到的事件向未来发生的事件推断,并使用统计模型拟合适合适合罕见事件的随机模型。这样的模型涉及泊松点过程,常规变化,一般空间和随机集的随机过程,其估计需要现代统计数据中的高级思想。最近的应用包括估计未来热浪或冷扣的大小和程度,极端降雨和降雪的时空建模,河流网络点的关节洪水的概率,风暴和闪电袭击的电站风险以及财务应用。
EEL-508课程标题:机器学习-LTP:3-1-0
课程概述:概率,随机变量和随机信号的概念。随机过程的一阶和二阶统计。事件点的泊松分布。随机变量及其特征。CDF&PDF及其属性。存在定理。高斯RV,Poisson RV,Bernoulli分布的RV和均匀分布的RV,线性系统对随机信号输入的响应;功率密度光谱和基本关系。线性馈回控制的分析设计。parseval的定理及其概括。M.S.E. 对不同情况的估计。 维纳蹄积分方程和解决方案方法。 高斯 - 马尔可夫序列和过程模型;连续和离散线性系统的最佳预测,过滤和平滑。M.S.E.对不同情况的估计。维纳蹄积分方程和解决方案方法。高斯 - 马尔可夫序列和过程模型;连续和离散线性系统的最佳预测,过滤和平滑。
人工智能 (AI) 和机器学习的基本数学...
简单来说,可观测性驱动着任何随机过程的概率特征。让 X t 成为离散状态变量,其值可以用整数 1,…S 表示,其中 S 是可能状态的数量。转换模型 p(X t |X t-1 ) 变为 SxS 矩阵 T,其中 T ij = p(X t =j | X t-1 =i),T ij 是从 i 状态转换到 j 状态的概率。在这里,为了解决转换问题,我们通常将传感器模型置于矩阵形式,其中 e t 是时间 t 的证据变量,需要为每个状态使用 p(e t |X t =i) 指定,对于每个状态 i,保持 (O t),第 i 个对角线项 p(e t |X t =i) 和其他值为 0。使用列向量后,前向和后向方程得出;
PHYSICAL REVIEW A 105, 013716 (2022) 现实...
我们描述了一种有效的数值方法,用于模拟存在失相和衰减的情况下相互作用的自旋系综的动力学。该方法基于孤立系统的离散截断维格纳近似,将自旋系综的平均场动力学与离散初始自旋值的蒙特卡罗采样相结合,以解释量子关联。在这里,我们展示了如何通过将确定性平均场演化替换为随机过程来将这种方法推广到耗散自旋系统,该过程描述了相干性和群体的衰减,同时保留了每个自旋的长度。我们展示了该技术在模拟非经典自旋压缩效应或具有 10 5 个相互作用的两级系统的腔 QED 模型的动力学和稳态中的应用。这为在现实实验室条件下对各种量子光学实验或固态自旋系综进行精确的实尺度模拟提供了可能性。
ECE 659智能传感器和传感器网络 通过及时的工程优化移动边缘AI生成的一切(AIGX)服务:基本,框架和案例研究 在6G网络中有效检索增强生成服务 随机过程.pdf
本课程旨在向学生介绍物联网系统设计,部署和管理中典型的基本主题和问题。它突出了我们社会中物联网发展的重要性,并研究了典型的物联网设备和网络的重要组成部分,并讨论了当前和未来的物联网趋势。该课程强调了AI在解决物联网网络复杂性,自我意识和大数据处理问题中的作用。还引入了IoT网络核心的主题,包括数据融合,同步,云计算,本地化,嵌入式/小型AI和图形信号处理,压缩传感,聚类和IOT分析,分析和IOT分析,区块链及其在IoT中的应用。传感器网络将被用作物联网中的新兴应用程序。
关于量子随机游动
正如标题所示,以下论文是对当前正在进行的量子随机游动研究的一次全面但绝不完整的探索。经典随机游动在 20 世纪初被引入并形式化,作为建模和研究金融以及物理或生物现象的工具。著名的布朗运动最早由法国数学家 Louis Bachelier 于 1900 年在其博士论文《投机理论》中描述,当时他试图研究巴黎证券交易所的价格变化。从那时起,Henri Lebesgue、Émile Borel、Paul Lévy 等人发展了测度理论,从而对随机游动等随机过程进行了严格的定义。简而言之,随机游动是某些数学空间(如图、群或向量空间)中的随机路径。第 2 章将介绍相关定义以及随机游动极限行为的定理,因为我们对经典设置与量子理论设置的区别感兴趣。
维特比算法 - 巴黎矿业
P I HE 维特比算法 (VA) 于 1967 年被提出作为卷积码解码的方法。从那时起,它就被认为是解决各种数字估计问题的有效方法,就像卡尔曼滤波器被应用于各种模拟估计问题一样。与卡尔曼滤波器一样,VA 使用递归方法跟踪随机过程的状态,该方法在某种意义上是最优的,并且易于实现和分析。然而,底层过程被假定为有限状态马尔可夫而不是高斯,这导致了结构上的显著差异。本文主要旨在对 VA、其结构和分析进行教程介绍。它还旨在或多或少详尽地回顾截至本文撰写时(1972 年夏季)所有受该算法启发或与该算法相关的工作。我们相信该算法将在越来越多的领域得到应用。我们希望能够为本文的读者加速这一进程。