XiaoMi-AI文件搜索系统
World File Search System平均场
无限视野的深度加固学习...
摘要。我们介绍了旨在以统一的方式解决连续空间均值场（MFG）和平均场控制（MFC）问题的增强学习算法的开发和分析。所提出的方法通过参数化的分数函数将参与者 - 批判性（AC）范式与平均场分布的表示形式配对，可以以在线方式进行有效更新，并使用Langevin Dynamics从产生的分布中获取样品。AC代理和分数函数被迭代更新以收敛到MFG平衡或给定平均领域问题的MFC Optimum，具体取决于学习率的选择。算法的直接修改使我们能够求解混合的均值场控制游戏。使用在有限的地平线框架中使用线性界面基准来评估我们的算法的性能。
![arxiv：2307.04700V2 [Physics.Soc-PH] 3 Jul 2024](/simg/d\d16bcf9abe5e2671c07b62620efa839dd7bfb24b.webp)
arxiv：2307.04700V2 [Physics.Soc-PH] 3 Jul 2024
当人口的一部分变得不受传染病的免疫力时，由于集体保护（称为牛群的免疫力），人口范围的感染风险会降低。基于平均场模型的研究表明，异质种群中的自然感染可能比均质免疫更有效地诱导群免疫。在这里，我们使用网络流行模型来表明情况也相反。我们确定了引起疾病引起的群体免疫力的两种相互竞争的机制：社会活性个体中的高度免疫力增强了牛群的免疫效应，而免疫Insividuals的拓扑定位却削弱了它。在嵌入低维空间中的网络中定位的效果更强，这可以使疾病诱导的免疫力比随机免疫效率降低。我们的结果突出了网络在塑造牛群免疫中的作用，并呼吁仔细检查为公共卫生政策提供信息的模型预测。
JHEP11（2024）156
这项工作调查了可符合性（3Þ1） - 二维nambu - Jona-Lasinio（NJL）模型的相结构，特别关注不均匀阶段（IPS），在该阶段（IPS）中，手掌凝结物在空间上是不均匀的，在空间上是不均匀的，密切相关的Moat Moat Companimes，在这里，在这里，有偏见的不合情对离的偏爱不合适的人类关系。我们使用平均场近似值，并考虑五个不同的正则化方案，包括三个晶格离散化。为了研究IP对正则化方案和调节剂价值的选择的依赖性，对不同正则化方案内的结果进行了系统的分析。IP对所选的正则化方案表现出极大的依赖性，该方案在该模型中对不均匀阶段的结果进行了任何物理解释。相比之下，我们发现护城河制度的一个温和的方案依赖性表明其存在是NJL模型及其对称性的作用的结果，因此它也可能存在于QCD中。
Quantum Vibes - 2024 年第二季度
然而，超导体中的二极管效应可能由几种不同的机制引起，具体取决于器件的成分和结构。几个研究小组已经研究了 SDE 理论。例如，通过使用平均场、Bogoliubov-de Gennes (BdG) 和 Ginzburg-Landau 理论，最近提出了无结块体超导体中的 SDE 以及其约瑟夫森结版本的理论见解。然而，另一个重要概念是邻近耦合，其中约瑟夫森结是在高自旋轨道耦合材料之上制造的；在这里，反演对称性不仅被器件的异质成分破坏，还被自旋轨道耦合项破坏；在这里，破坏 TRS 所需的磁场位于器件平面内。近年来，自旋轨道耦合非中心对称超导体中 SDE 的有趣实验演示已经复兴并刺激了非互易超电流传输的理论研究。然而，SDE 的想法已经存在了几十年。
海马CA1
在计算神经科学中，脑微电路和区域的生物学现实模型的发展是一个非常相关的主题。从基础研究到临床应用，对准确的模块的需求不断增长，该模型融合了局部细胞和网络特异性，能够捕获与给定大脑区域相关的广泛动态和功能。这些模型的主要挑战之一是不同尺度之间的通过，从微观（蜂窝）到中索（MicroCircuit）和Macroscale（区域或全脑级别），同时在同时限制计算资源的需求。解决此问题的一种新颖方法是使用神经元活动的平均场模型来构建大规模的模拟。这为相对较低的计算需求之间的量表之间的通过提供了有效的解决方案，这是由于系统维度的急剧降低而实现的。在本文中，我们引入了海马CA1的多尺度模拟框架，这是大脑的一个区域
量子引力以暗粒子形式局部大规模激发
我们渐近地构造了一个静态球形激发态，该激发态在可重正化量子引力中无奇点，具有无背景性质。其直径由量子引力的关联长度给出，比普朗克长度长 2 个数量级，外部有史瓦西尾。内部的量子引力动力学采用非微扰高阶修正表达式来描述，该表达式假设了动力学在强耦合的边缘消失的物理要求。运行耦合常数是非线性和非局域性的表现，通过将其近似为依赖于径向坐标的平均场来管理。如果质量是普朗克质量的几倍，我们可以建立一个包含运行效应的引力势线性化运动方程组，并获得激发态作为其解。它可能是暗物质的候选者，并将为黑洞物理学提供新的视角。
选修课程 - TU 登录门户 - 特里布万大学
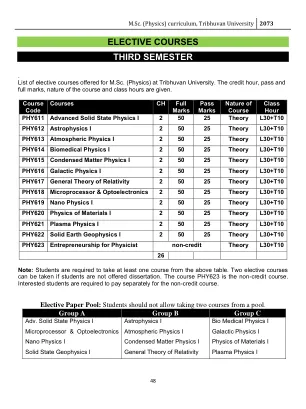
物理学。课程内容：1. 简介：[2 小时] 1.1 非相互作用电子气。2. Born-Oppenhemier 近似：[3 小时] 2.1 基本哈密顿量，2.2 绝热近似，2.3 简化电子问题。3. 二次量子化：[5 小时] 3.1 玻色子，3.2 费米子，3.3 费米子算符。4. Hartree-Fock 近似：[4 小时] 4.1 非相互作用极限，4.2 Hartree-Fock 近似，4.3 图表。5. 相互作用电子气：[4 小时] 5.1 均匀电子气，5.2 Hartree-Fock 激发谱，5.3 金属的结合能。 6. 金属中的局部磁矩：[4 小时] 6.1 局部矩：现象学，6.2 平均场解。 7. 局部矩的猝灭：[8 小时] 7.1 近藤问题，7.2 近藤汉密尔顿量，7.3 为什么 J 为负？ 7.4 散射和电阻率最小值，7.5 电子-杂质散射振幅，7.6 近藤温度。
量子广义 Potts-Hopfield 神经网络的相图
摘要 我们介绍并分析了 q 状态 Potts-Hopfield 神经网络 (NN) 的开放量子泛化，这是一种基于多层经典自旋的联想记忆模型。这个多体系统的动力学以 Lindblad 型马尔可夫主方程的形式表示，该方程允许将概率经典和相干量子过程平等地结合起来。通过采用平均场描述，我们研究了由温度引起的经典涨落和由相干自旋旋转引起的量子涨落如何影响网络检索存储的记忆模式的能力。我们构建了相应的相图，在低温状态下，该相图显示的模式检索类似于经典的 Potts-Hopfield NN。然而，当量子涨落增加时，会出现极限环相，而极限环相没有经典对应相。这表明量子效应可以相对于经典模型从质上改变稳态流形的结构，并可能允许人们编码和检索新类型的模式。
![arxiv：2403.03025v1 [cond-mat.supr-con] 5 2024年3月5日](/simg/f\fc80240db4e3dd063bfc257813fb4d33c3f355e4.webp)
arxiv：2403.03025v1 [cond-mat.supr-con] 5 2024年3月5日
对2D超导体的最新实验允许表征临界温度和跨BCS-BEC交叉的相位图作为密度的函数。我们从这些实验中获得了低温下超导状态的微观参数，通过BCS平均场接近。对于Li X Zrncl，提取的参数用于评估超导相位刚度和BEREZINSKII-KOSTERLITZ-thouless-thouless（BKT）临界温度，通过实现相应的重新分配组（RG）方法，整个BCS-BEC交叉中的临界温度。通过这种方式，我们对BKT理论的预测能力进行定量测试，以评估临界温度。RG流动方程证明对相位刚度和临界温度的重大重新归一化，这对于获得BKT理论与实验之间的令人满意的一致性至关重要，尤其是在BCS-BEC交叉方面。我们预测温度范围可以在BCS-BEC跨界的Li X Zrncl中测量相位刚度重归于。与其他超导性的其他微观理论相反，我们发现可以利用BKT理论来定量评估不同配对方案中2D超导体的临界温度。
走向量子计算机的密度泛函理论？
量子计算机已显示出解决传统计算机目前无法解决的特定问题的潜力，但它们在比传统计算机更快地解决工业问题方面仍处于起步阶段[1,2]。量子计算机的近期应用之一是量子化学（见参考文献[3-7]及其参考文献），其重点是波函数理论（WFT），旨在对电子结构问题进行数值精确解。虽然量子相位估计（QPE）算法原则上能够完全解决该问题[8-12]，但所需的电路深度阻碍了它们在嘈杂的中尺度量子（NISQ）时代的应用[13]。因此，人们开发出了更有效的算法，例如量子随机漂移协议 [ 14 ] ，或使用幺正函数的线性组合和量子比特化形式直接模拟哈密顿量 [ 15 – 18 ] 。为了更适应 NISQ 时代，人们专门设计了几种变分量子算法（混合量子-经典），用于制备基态 [ 19 – 23 ] 和最近的激发态 [ 24 – 26 ] ，并计算原子力和分子特性 [ 27 – 30 ] 。然而，尽管量子计算机宣布了指数级的加速，但何时才能真正在实践中实现实际的量子优势仍不清楚，而且在不久的将来期待任何有重大影响的应用都是困难的 [ 31 – 34 ] 。事实上，量子算法在量子化学中的应用仍然受到可负担系统规模的限制，因为系统的大小决定了所需的量子比特数。尽管量子设备上的量子比特数有望迅速增加，但未来几年预计还不会出现能够处理真实量子化学系统的稳定机器。在 NISQ 时代的噪声量子计算机中，高精度结果是难以实现的，对于具有重大社会和工业影响的相关应用来说，对化学精度的追求仍然是一条漫长的道路。目前，对化学、凝聚态物理甚至生物学等大型系统的经典计算主要依赖于密度泛函理论 (DFT) [ 35 , 36 ]，由于它仅相对于系统尺寸以立方倍数缩放，因此不能预先预期其具有量子优势。相反，最近的研究重点是利用矩阵积态、机器学习和量子计算机构建精确的交换关联 (XC) 密度泛函，而这种密度泛函的精确确定是 QMA 难题 [37]。人们还研究了如何解决 Kohn-Sham 势反演问题，其中在量子计算机上测量随时间演化的多体系统的密度 [44-46]。其他有趣的工作分别将 DFT 及其时间相关版本的 Hohenberg-Kohn 定理和 Runge-Gross 定理推广到量子比特哈密顿量，从而有可能将量子计算中的多体可观测量近似为密度的单量子比特量函数 [ 47 , 48 ]。但上述工作均未旨在解决量子计算机上的 Kohn-Sham (KS) 非相互作用问题。只有少数尝试在量子计算机上执行平均场近似，例如在 12 量子比特平台上具有里程碑意义的 Hartree-Fock 实验 [ 49 ]，或在量子退火器上计算单粒子密度矩阵 [ 50 ]。在这两种情况下，都没有预见到实际的量子优势。因此，DFT 仍然应用于经典计算机，尽管有时通过使用嵌入策略在量子计算机上与 WFT 结合 [ 6 , 51 , 52 ]。在这项工作中，我们研究了使用数字量子计算机扩展 DFT 等平均场型方法的好处。讨论了一种可能的量子优势，即 KS 汉密尔顿量与辅助相互作用汉密尔顿量之间的反直觉映射，以计算基础表示，这与几十年来的做法相反。有了这种新的编码，在某些理想情况下，平均场型汉密尔顿量可以在量子计算机上以指数级的速度得到解决，类似于相互作用汉密尔顿量。