XiaoMi-AI文件搜索系统
World File Search System截断量子态的纠缠
纠缠是量子力学的定义特征之一,也是许多量子信息协议的基本资源 [1]。许多理论和实验研究都致力于研究一对二能级系统(量子比特)的纠缠。高维(量子比特)系统的二分纠缠研究较少。然而,从根本上讲,更好地理解纠缠量子比特可以澄清量子物理的一些微妙之处。例如,与量子比特相比,量子比特被证明可以增强非经典效应,因为它们允许更强的局部现实主义违反 [2, 3]。此外,从更务实的角度来看,高维量子态比简单量子比特具有更高的信息容量,并允许量子密钥分发协议容忍更高的噪声阈值 [4]。在光子系统中,(纠缠)量子比特被编码在高维(最终是无限维)希尔伯特空间的有限维子空间中。这可以通过使用空间模式(例如轨道角动量 [5, 6, 7])或离散化连续自由度(例如频率 [8, 9] 或时间 [10, 11])来实现。此外,这种最初有限维的状态可以在其动态演化过程中扩展到整个希尔伯特空间。例如,当光子轨道角动量携带状态 [12] 通过自由空间 [13, 14, 15, 16] 或光纤 [17] 传输时,就是这种情况。然而,输出状态通常被投射到
通过截断泰勒级数进行汉密尔顿模拟的 NISQ 算法
人们认为,模拟多体量子系统的动力学是量子计算机能够显示出优于传统计算机的量子优势的首批领域之一。噪声中型量子 (NISQ) 算法旨在有效利用当前可用的量子硬件。对于量子模拟,已经提出了各种类型的 NISQ 算法,它们各有优势,也各有挑战。在这项工作中,我们提出了一种新算法,即截断泰勒量子模拟器 (TQS),它继承了现有算法的优点并减轻了一些缺点。我们的算法没有任何经典量子反馈回路,并通过构造绕过了荒芜高原问题。我们的混合量子经典算法中的经典部分对应于具有单个二次等式约束的二次约束二次规划 (QCQP),它允许半定松弛。基于 QCQP 的经典优化最近被引入作为量子辅助特征值求解器 (QAE) 中的经典步骤,QAE 是用于汉密尔顿基态问题的 NISQ 算法。因此,我们的工作为汉密尔顿基态问题的 NISQ 算法和汉密尔顿模拟提供了概念上的统一。我们将基于微分方程的 NISQ 算法(如量子辅助模拟器 (QAS) 和变分量子模拟器 (VQS))恢复为我们算法的特例。我们在当前云量子计算机上的一些小例子上测试了我们的算法。我们还提供了一种系统的方法来提高我们算法的准确性。
关于右截断威布尔分布和幂函数分布最小值的注记
[1] Bobotas, P. 和 Koutras, MV (2019)。随机变量随机数的最小值和最大值的分布,《统计与概率快报》,第 146 期,第 57-64 页。[2] Ferreira, MA 和 Andrade, M. (2011)。M/G/∞ 队列繁忙期分布指数,《应用数学杂志》,第 4 (3) 期,第 249-260 页。[3] Forbes, C.;Evans, M.;Hastings, N. 和 Peacock, B. (2011)。《统计分布》,第四版,John Wiley & Sons, Inc.,新泽西州霍博肯。[4] Jodr´a, P. (2020)。根据移位 Gompertz 定律得出的有界分布,《沙特国王大学杂志 - 科学版》,第 32 期,第 523-536 页。 [5] Jodr´a, P. 和 Jim´enez-Gamero, MD 基于指数几何分布的有界响应分位数回归模型,REVSTAT 统计期刊,18(4),415-436。[6] Johnson, NL;Kotz, S. 和 Balakrishnan, N. (1994)。连续单变量分布,第 1 卷第二版,John Wiley & Sons, Inc.,纽约。[7] Mart´ınez, S. 和 Quintana, F. (1991)。广义上截断威布尔分布的检验,统计和概率快报,12(4),273-279。[8] McEwen, RP 和 Parresol, BR (1991)。完整和截断威布尔分布的矩表达式和汇总统计数据,《统计通讯 – 理论与方法》,20(4),1361-1372。[9] Meniconi, M. 和 Barry, DM (1996)。幂函数分布:一种用于评估电气元件可靠性的有用而简单的分布,《微电子可靠性》,36(9),1207-1212。[10] Nadarajah, S.;Popovi´c, BV 和 Risti´c, MM (2013)。Compounding:一个用于计算通过复合连续和离散分布获得的连续分布的 R 包,《计算统计学》,28(3),977-992。[11] Prabhakar, DN;Xie, M. 和 Jiang, R. (2004)。威布尔模型,《概率和统计学中的威利级数》,Wiley-Interscience,John Wiley & Sons,Inc.,新泽西州霍博肯。[12] Rao,ASRS(2006 年)。关于右截断瑞利分布生成函数推导的注记,《应用数学快报》,19(8),789-794。[13] Rinne,H.(2009 年)。《威布尔分布手册》,CRC Press,博卡拉顿。[14] Silva,RB;Bourguignon,M.;Dias,CRB 和 Cordeiro,GM(2013 年)。扩展威布尔幂级数分布的复合类,《计算统计与数据分析》,58,352-367。[15] Tahir,MH;Alizadeh,M.;Mansoor,M; Gauss, MC 和 Zubair, M. (2016)。威布尔幂函数分布及其应用,《Hacettepe 数学与统计杂志》,45(1),245-265。[16] Wingo, DR (1988)。右截断威布尔分布与寿命测试和生存数据的拟合方法,《生物统计学杂志》,30(5),545-551。[17] Wu, Z.;Kazaz, B.;Webster, S. 和 Yang, KK (2012)。交货时间和需求不确定性下的订购、定价和交货时间报价,《生产与运营管理》,21,576-589。[18] Zhang, T.和 Xie, M. (2011). 论上截断威布尔分布及其可靠性含义,可靠性工程与系统安全,96,194–200。
用截断泰勒级数制备变分量子吉布斯态
量子吉布斯态的制备是量子计算的重要组成部分,在量子模拟、量子优化和量子机器学习等各个领域都有广泛的应用。在本文中,我们提出了用于量子吉布斯态制备的变分混合量子-经典算法。我们首先利用截断泰勒级数来评估自由能,并选择截断自由能作为损失函数。然后,我们的协议训练参数化量子电路以学习所需的量子吉布斯态。值得注意的是,该算法可以在配备参数化量子电路的近期量子计算机上实现。通过进行数值实验,我们表明只需一个额外量子位的浅参数化电路就可以训练来制备保真度高于 95% 的伊辛链和自旋链吉布斯态。具体来说,对于伊辛链模型,我们发现仅具有一个参数和一个附加量子位的简化电路假设可以被训练以在逆温度大于 2 时实现吉布斯态制备的 99% 保真度。
通过电荷检测质谱法分析AAV提取的DNA揭示了基因组截断
摘要:腺相关病毒(AAV)是一种广泛使用的基因治疗载体。完整包装的基因组是有效治疗的关键质量属性,是必要的。在这项工作中,使用电荷检测质谱法(CDM)来测量从重组AAV(RAAV)向量提取的感兴趣基因组(GOI)的分子量(MW)分布。将测得的MWS与具有不同的Gois,血清型和生产方法(SF9和HEK293细胞系)的RAAV载体的序列质量进行了比较。在大多数情况下,测得的MW略大于序列质量,结果归因于柜台。但是,在少数情况下,测得的MW明显小于序列质量。在这些情况下,基因组截断是差异的唯一合理解释。这些结果表明,CDM对提取的GOI的直接分析提供了一种快速而有力的工具,可以评估基因组完整性中的基因组完整性。■简介
不确定性驱动的轨迹截断,用于数据增强的数据加强学习
摘要。配备了训练有素的环境动态,基于模型的型号增强学习(RL)算法可以成功地从固定尺寸的数据集中成功学习良好的策略,甚至有些质量较差的数据集。不幸的是,不能保证从训练有素的动态模型中生成的样品是可靠的(例如,某些合成样本可能位于静态数据集的支持区域的外面)。为了解决这一点,我们提出了与u ncleantity(tatu)的束缚t runcation,如果沿轨迹的累积不确定性太大,则可以自适应地截断合成轨迹。我们从理论上展示了塔图的绩效界限,以证明其受益合理。为了示出Tatu的优势,我们首先将其与两种基于经典模型的型号RL算法结合在一起,MOPO和组合。此外,我们将tatu与几个未经省的模型集成在一起,不含频率rl算法,例如BCQ。D4RL基准测试的实验结果表明,Tatu显着提高了其能力,通常会大幅度通过很大的边缘。代码可在此处找到。
purcell增强的单光子发射从量子点耦合到截断的高斯微腔
purcell增强量子点(QD)单光子发射和设备亮度的增加,已经证明了各种类型的微腔。在这里,我们提出了第一个实现截断的高斯形状的微腔与QD的截断。实施基于湿化学蚀刻和外延半导体过度生长。实验研究了腔模式及其空间纤维,并与模拟很好地吻合。可以通过制造设计可重复控制具有6000张Q-因子的基本模式波长,而29 L EV的小极化分裂可以重复控制,从而使腔体适应了特定的QD。最后,通过温度调节对腔内QD的过渡进行调节和关闭共振。在共振上减少了一个以上的因子减少的衰减时间清楚地表明purcell的增强,而G(2)(0)¼0.057的二阶相关测量结果证明了QDS单光子特性得以保留。
一种新型的滴定截断变体,与日本家庭中的家族性扩张心肌病有关,其功能分析在基因组编辑的mod中
摘要扩张的心肌病(DCM)是心力衰竭的常见原因。ttn是DCM的代表性致病基因,主要作为截断变体呈现。但是,在健康个体中也发现了TTN截断变体,因此评估每个变体的致病性很重要。在这项研究中,我们分析了一名男性日本患者的67个心肌病相关基因,该患者因复发性严重心力衰竭而住院,并确定了一种新型的截断变体TTN SER17456ARG FS*14。此TTN截断变体位于A波段区域。此外,患有心力衰竭的患者的母亲具有相同的变体,而父亲和没有心力衰竭的兄弟并没有带有这种变体。检查与截断变体相关的功能变化,对H9C2细胞进行了基因组编辑,以生成具有同源截断变体的细胞。使用全反击甲酸分化细胞,发现骨骼肌肌动蛋白和心肌动蛋白的mRNA表达分别增加和减少,与DCM或心力衰竭患者的已知变化一致。相比之下,用作对照的另一个带有Titin截断变体的细胞显示与心力衰竭相关的基因没有变化。总而言之,我们在家族性DCM患者中发现了一种新型的TTN截断变体,并使用相对简单的细胞模型证实了其功能变化。新型截断变体被确定为致病性和致病突变。(int heart j Advance出版)关键词:基因组编辑,心力衰竭
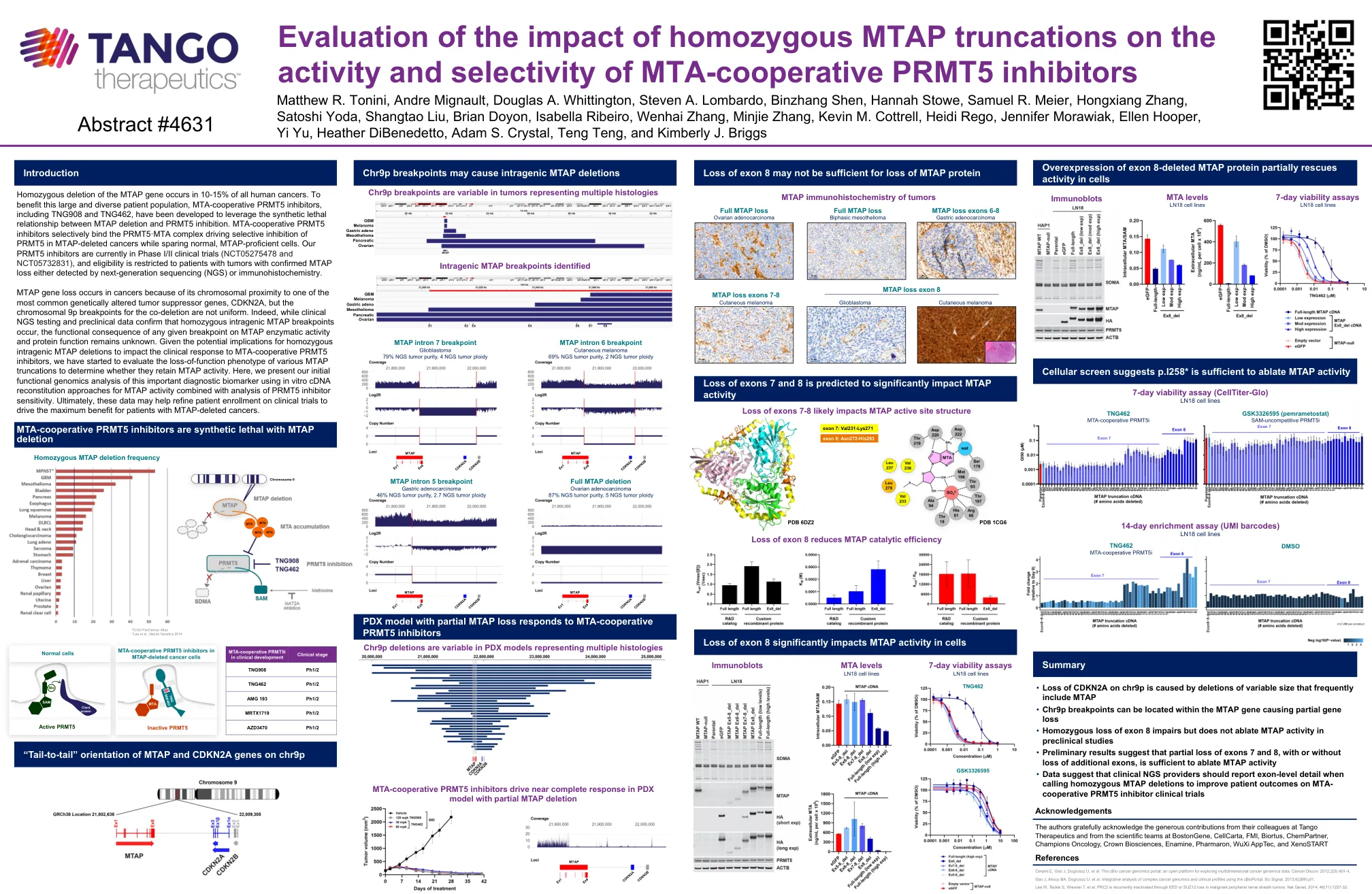
评估纯合MTAP截断对MTA合作PRMT5抑制剂的活性和选择性的影响
MTAP基因的纯合缺失发生在所有人类癌症中的10-15%中。为了使包括TNG908和TNG462在内的MTA合作PRMT5抑制剂受益,已开发出来的MTA合作PRMT5抑制剂,以利用MTAP缺失与PRMT5抑制之间的合成致死关系。MTA合并PRMT5抑制剂选择性地结合了PRMT5抑制剂在MTAP骨骼骨骼癌中的PRMT5驱动选择性抑制,同时保留正常的MTAP且可培养的细胞。我们的PRMT5抑制剂目前正在I/II期临床试验(NCT05275478和NCT05732831)中,并且资格仅限于具有确认的MTAP损失的肿瘤患者,即通过下一代测序(NGS)或免疫组织化学化学。mTAP基因丧失发生在癌症中,因为它与最常见的遗传改变的肿瘤抑制基因CDKN2A的染色体接近,但是共脱落的染色体9p断点并不均匀。的确,尽管临床NGS测试和临床前数据证实了纯合性内部MTAP断点,但MTAP酶活性和蛋白质功能上任何给定断点的功能后果仍然未知。鉴于对纯合基因内MTAP缺失的潜在影响会影响对MTA合件PRMT5抑制剂的临床反应,我们已经开始评估各种MTAP截断的功能丧失表型,以确定它们是否保留MTAP活性。在这里,我们使用体外cDNA重构方法与PRMT5抑制剂敏感性分析,对这种重要的诊断生物标志物进行了最初的功能基因组学分析。最终,这些数据可能有助于完善患者参加临床试验的入学率,以促进MTAP骨骼癌症患者的最大收益。