XiaoMi-AI文件搜索系统
World File Search System特征值
线性方程组的 HHL 算法 - PhysLab
HHL 算法由 Aram Harrow、Avinatan Hassidim 和 Seth Lloyd 于 2009 年提出，用于利用量子计算原理求解线性方程组。为了求解这样的系统，我们将问题表示为 A | x ⟩ = | b ⟩ 的形式，其中 | x ⟩ 和 | b ⟩ 是归一化向量，A 是厄米矩阵。该过程涉及利用量子相位估计 (QPE) 子程序查找矩阵的特征值。这反过来又利用了逆量子傅里叶变换 (QFT)。然后使用确定的特征值实现受控旋转，以有效地找到矩阵 A 的逆。这使我们能够计算 | x ⟩ = A − 1 | b ⟩ 。最后一步是取消计算相位估计。接下来我们讨论该算法在物理硬件上的逐步实现，并在IBM量子计算机上模拟结果。最后，我们将经典算法的运算次数与有望大幅提高计算速度的HHL算法进行比较。
![arXiv:2011.11511v1 [cond-mat.mtrl-sci] 2020 年 11 月 23 日](/simg/2\22f9ab58d425bf8a2a541263a12de9452579352d.webp)
arXiv:2011.11511v1 [cond-mat.mtrl-sci] 2020 年 11 月 23 日
现今许多科学家在量子纳米和微电子器件的投影或实验[1, 2]中采取的方法都是努力寻找由于所涉及电现象维度长度缩放而引起的物质量子本征态的解。哈密顿量[5–7]方法用于理论求解该问题，需要写出特征值微分方程，这些方程可以通过现代计算技术求解。我们将在解决问题的过程中纳入这些方法，以简化投影过程本身。许多作者[8–11]提出了几项工作，但尚未给出明确的基于 DFT[3, 4]的特征值方程，本文通过扩展 Kohn-Sham 微分方程的变分方法找到了该方程。下一节将介绍几个由量子方程求解引起的问题，这些问题主要是在无限周期系统或由有限或周期性复制品制成的有限物质采样的背景下寻找解决方案。本文的最后一部分将报告结论。
在完整的两部分图上计数量子
量子计数是一种关键量子算法，旨在确定数据库中标记元素的数量。该算法基于量子相估计算法，并使用Grover算法的进化算子，因为其非平凡特征值取决于标记元素的数量。由于Grover的算法可以看作是在完整图上的量子步行，因此扩展量子计数的自然方法是在不完整的图上使用基于量子 - 步行的搜索的进化运算符，而不是Grover的运算符。在本文中，我们通过分析具有任意数量的标记顶点的完整两分图上的量子步行来探讨此扩展。我们表明，进化运算符的某些特征值取决于标记的顶点的数量，并且使用此事实，我们表明量子相估计可用于获得标记的顶点的数量。与我们的算法与原始量子计数算法紧密相位的两分图中标记顶点数量的时间复杂性。
量子信息理论解决方案 7。
(d) 如果对二分态 ρ AB 的 A 或 B 施加部分转置，且至少有一个负特征值，则 ρ AB 不可分离，即必须纠缠。如果 ρ AB 的部分转置为正，则无法判断该状态是否纠缠（除非在 2 × 2 或 2 × 3 维度上，如上所述）。
![arXiv:2312.14786v2 [quant-ph] 2024 年 3 月 18 日](/simg/4\42f462c121efd0b7b1fdedc48645d7e481724129.webp)
arXiv:2312.14786v2 [quant-ph] 2024 年 3 月 18 日
块编码是最近开发的量子信号处理的关键要素，它构成了量子算法的统一框架。量子信号处理最初是为了简化和优化搜索、振幅估计和汉密尔顿模拟等多个问题的资源利用而展示的，但其能力远不止于此，可能为设计新的量子算法提供尚未开发的潜力。在本文中，我们利用块编码大大增强了两种之前提出的量子算法：最大特征值估计和量子梯度下降。与之前涉及复杂程序的研究不同，我们使用单元块编码的研究结果表明，即使使用基本操作，这些新改进的算法也可以摆脱原始算法中存在的主要缩放因子。这产生了更高效的量子算法，能够以惊人的效率解决复杂的计算问题。此外，我们还展示了如何将我们提出的方法扩展到不同的环境，包括矩阵求逆和多特征值估计。
R22 B.Tech. CSE（AI 和 ML）课程大纲 JNTU 海得拉巴
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I：矩阵 10 L 通过梯形和标准形式对矩阵进行秩，通过高斯-乔丹方法对非奇异矩阵进行逆运算，线性方程组：用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元：特征值和特征向量 10 L 线性变换和正交变换：特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理（无证明）、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元：微积分 10 L 均值定理：罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积（仅限于笛卡尔坐标系）、不当积分的定义：Beta 函数和 Gamma 函数及其应用。第四单元：多元微积分（偏微分和应用）10 L 极限和连续性的定义。偏微分：欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用：使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
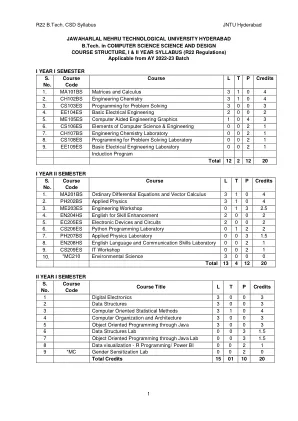
R22 B.Tech. CSD 教学大纲 JNTU 海得拉巴 1 ...
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I：矩阵 10 L 通过梯形和标准形式对矩阵进行秩，通过高斯-乔丹方法对非奇异矩阵进行逆运算，线性方程组：用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元：特征值和特征向量 10 L 线性变换和正交变换：特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理（无证明）、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元：微积分 10 L 均值定理：罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积（仅限于笛卡尔坐标系）、不当积分的定义：Beta 函数和 Gamma 函数及其应用。第四单元：多元微积分（偏微分和应用）10 L 极限和连续性的定义。偏微分：欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用：使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
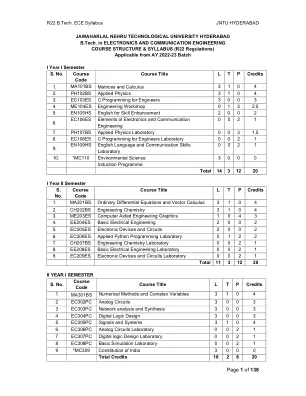
R22 B.Tech. ECE 教学大纲 JNTU 海得拉巴
写出一组线性方程的矩阵表示并分析方程组的解 寻找特征值和特征向量 利用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数求不当积分 找出有/无约束的两个变量函数的极值。 评估多重积分并应用概念寻找面积、体积 UNIT-I：矩阵 10 L 通过梯形和标准形式对矩阵进行秩计算，通过高斯-乔丹方法对非奇异矩阵进行逆计算，线性方程组：通过高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元：特征值和特征向量 10 L 线性变换和正交变换：特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理（无证明）、利用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、利用正交变换将二次型简化为标准形式。 第三单元：微积分 10 L 均值定理：罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积（仅在笛卡尔坐标系中）、不定积分的定义：Beta 函数和 Gamma 函数及其应用。 UNIT-IV：多元微积分（偏微分和应用）10 L 极限和连续性的定义。偏微分：欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用：使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
太阳能职业学士
第 2 单元：代数和超越方程的解：迭代法 - 二分法、假位置法（Regula Falsi 方法）、不动点迭代法、牛顿拉夫森法、广义牛顿法、拉马努金法、穆勒法；加速收敛 - Aitken 方法、Graeffe 根平方法、复根。第 3 单元：矩阵：矩阵运算：加法、减法和乘法。矩阵、矩阵的转置、矩阵的逆、矩阵的秩、向量和矩阵范数、特征值问题：对称三对角矩阵的特征值、Householder 方法、QR 方法。第 4 单元：线性方程组的解：高斯消元法、高斯-乔丹法；非线性方程组的解：不动点迭代法、牛顿-拉夫森法，书籍：1. 数值分析入门方法，SS Sastry，Prentice Hall India，第 3 版。2. 计算机在物理学中的应用，Suresh Chandra，Narosa 3. 计算机导向数值方法，V. Rajaraman，第 3 版。1GP4-电子实验室。（实用）