XiaoMi-AI文件搜索系统
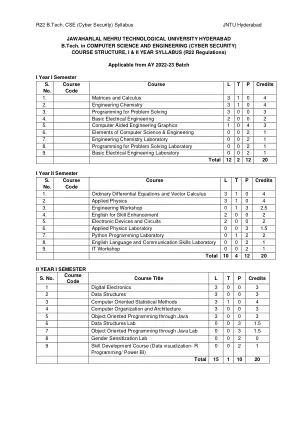
World File Search System特征向量
R22 B.Tech. CSE（网络安全）课程大纲
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I：矩阵 10 L 通过梯形和标准形式对矩阵进行秩，通过高斯-乔丹方法对非奇异矩阵进行逆运算，线性方程组：用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元：特征值和特征向量 10 L 线性变换和正交变换：特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理（无证明）、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元：微积分 10 L 均值定理：罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积（仅限于笛卡尔坐标系）、不当积分的定义：Beta 函数和 Gamma 函数及其应用。第四单元：多元微积分（偏微分和应用）10 L 极限和连续性的定义。偏微分：欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用：使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
使用基于迁移学习的特征提取和卷积神经网络进行基于脑电图的情绪识别
摘要。本文介绍了一种基于脑电图 (EEG) 的情绪识别新方法。该方法使用迁移学习从多通道脑电图信号中提取特征，然后将这些特征排列在 8×9 的图中以表示它们在头皮上的空间位置，然后我们引入一个 CNN 模型，该模型接收空间特征图并提取脑电图通道之间的空间关系并最终对情绪进行分类。首先，将脑电图信号转换为频谱图并通过预先训练的图像分类模型从脑电图频谱中获取特征向量。然后，重新排列不同通道的特征向量并将其作为 CNN 模型的输入，该模型提取空间特征或通道依赖关系作为训练的一部分。最后，CNN 输出被展平并通过密集层以在情绪类别之间进行分类。在本研究中，SEED、SEED-IV 和 SEED-V EEG 情绪数据集用于分类，我们的方法通过五倍交叉验证在 SEED 上实现了 97.09% 的最佳分类准确率，在 SEED-IV 上实现了 89.81% 的最佳分类准确率，在 SEED-V 数据集上实现了 88.23% 的最佳分类准确率。
使用个性化记忆对阿尔茨海默病进行纵向脑 MR 图像建模
摘要 对疾病进行纵向分析是了解其进展、设计预后和早期诊断工具的重要问题。从多个时间点收集数据的纵向图像中，可以捕获空间结构信息和纵向变化。时间动态比对症状的静态观察更具信息量，特别是对于阿尔茨海默病等神经退行性疾病，其进展跨越数年，早期变化微妙。在本文中，我们提出了一个新的生成框架来预测病变随时间的进展。我们的方法首先将图像编码为结构和纵向状态向量，其中可以执行时间轴上特征向量的插值或外推以操纵这些特征向量。这些处理后的特征向量可以解码到图像空间中，以预测我们感兴趣的时间点的图像。在训练期间，我们强制模型将纵向变化编码为纵向状态特征，并在单独的向量中捕获结构信息。此外，我们引入了个性化记忆的在线更新方案，使模型适应目标对象，从而帮助模型保留每个对象的大脑图像结构的细节。在公共纵向脑磁共振成像数据集上的实验结果证明了所提方法的有效性。
引用/参考：Tosun, M. & Çetin, O. (2021)。使用经验模态分解和 Welch 方法对四类运动幻像脑电信号进行深入分析
在基于脑电图（EEG）的脑机接口（BCI）应用中，从想象相关肢体运动获得的运动想象（MI）信号中提取特征并对其进行分类是一个非常重要的问题。在 MI-EEG 信号的研究中，已经使用了许多不同的特征提取方法和分类算法。然而，随着这些信号中类别数量的增加，分类成功率之间存在显著差异。在提出的方法中，提出了一种包括信号功率谱密度（PSD）信息的特征提取方法。通过对原始 EEG 数据应用经验模态分解 (EMD)，可以获得不同频率水平的信号。这些信号的PSD值是使用Welch方法计算的。将得到的PSD值组合成特征向量。使用生成的特征向量，训练了一种流行的深度学习算法——长短期记忆 (LSTM) 网络。对培训后获得的测试成功情况根据个人和渠道进行了详细的比较。比较结果发现，位于头皮中心点的通道比其他通道更成功。
同一旋转和量子混乱
摘要：我们表明，量子混乱的最重要度量，例如框架电势，争夺，Loschmidt Echo回声和超级阶段相关器（OTOC），可以通过异形旋转的统一框架来描述，即K-flold Unitary Channel的Haar平均值。我们表明，这样的措施可以始终以同感旋转的期望值的形式施放。在文献中，有时会通过频谱和其他时间通过汉密尔顿人产生动力学的特征向量来研究量子混乱。我们表明，借助这项技术，我们可以在可联合的哈密顿量和量子混沌汉密尔顿人之间平稳地插入。与特征向量稳定剂状态的哈密顿人的同一旋转不具有混乱的特征，这与那些从HAAR措施中获取特征向量的汉密尔顿人不同。作为一个例子，与通用资源相比，Clifford Resources腐烂到更高的值获得的OTOC。通过掺杂哈密顿人的非克利福德资源，我们在一类可集成模型和量子混乱之间的OTOC行为中显示了一个交叉。此外，利用随机矩阵理论，我们表明，量子混乱的这些度量清楚地将探针的有限时间行为与量子混乱区分为与高斯单位合奏（GUE）相对应的量子混乱，并将其与Poisson分布和高斯分布和高斯对数（Gaussian diagonal）（GDE）（GDE）（GDE）（gde）所给出的集成光谱。
R18 B.Tech. ECE 教学大纲 JNTU HYDERABAD 1
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 分析序列和级数的性质。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 UNIT-I：矩阵 矩阵：矩阵的类型，对称；Hermitian；斜对称；斜 Hermitian；正交矩阵；酉矩阵；通过梯形和标准形式对矩阵进行秩计算，通过高斯-乔丹方法求非奇异矩阵的逆；线性方程组；求解齐次和非齐次方程组。高斯消元法；高斯赛德尔迭代法。第二单元：特征值和特征向量线性变换和正交变换：特征值和特征向量及其性质：矩阵的对角化；凯莱-哈密尔顿定理（无证明）；用凯莱-哈密尔顿定理求矩阵的逆和幂；二次型和二次型的性质；用正交变换将二次型简化为标准形式第三单元：数列与级数序列：数列的定义，极限；收敛、发散和振荡数列。级数：收敛、发散和振荡级数；正项级数；比较检验、p 检验、D-Alembert 比率检验；Raabe 检验；柯西积分检验；柯西根检验；对数检验。交错级数：莱布尼茨检验；交替收敛级数：绝对收敛和条件收敛。 UNIT-IV：微积分中值定理：罗尔定理、拉格朗日中值定理及其几何解释和应用、柯西中值定理。泰勒级数。定积分在计算曲线旋转表面面积和体积中的应用（仅限于笛卡尔坐标系）、反常积分的定义：Beta 函数和 Gamma 函数及其应用。 UNIT-V：多元微积分（偏微分和应用）极限和连续性的定义。偏微分；欧拉定理；全导数；雅可比矩阵；函数依赖性和独立性，使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
MATH 361 线性代数
本课程介绍有限维抽象向量空间和线性变换的理论。主题包括：线性方程组、矩阵、矩阵代数、行列式和逆、线性组合和线性独立性、抽象向量空间、基和坐标变换、内积空间、正交基。我们还考虑线性变换、同构、线性映射的矩阵表示、特征值和特征向量、对角化和相似性。应用包括计算机图形学、马尔可夫链、化学、线性回归、网络流、电路和微分方程。
![arXiv:2302.11320v1 [quant-ph] 2023 年 2 月 22 日](/simg/g:\will\search\icon\source\0\0a2eb7025c71ddd96457925a514ed7ee47364a40.webp)
arXiv:2302.11320v1 [quant-ph] 2023 年 2 月 22 日
我们提出了量子选择配置相互作用 (QSCI)，这是一类混合量子经典算法，用于计算噪声量子装置上多电子哈密顿量的基态和激发态能量。假设可以在量子计算机上通过变分量子特征值求解器或其他方法准备近似基态。然后，通过在计算基础中对状态进行采样（这对于经典计算来说通常很难），可以识别出对再现基态很重要的电子配置。在经典计算机上，将这些重要配置所跨越的子空间中的哈密顿量对角化，以输出基态能量和相应的特征向量。可以类似地获得激发态能量。由于噪声量子装置仅用于定义子空间，因此结果对统计和物理错误具有鲁棒性，并且即使存在此类错误，所得的基态能量也严格满足变分原理。由于子空间中的显式特征向量是已知的，因此还可以估算出各种其他算子的期望值，而无需额外的量子成本。我们通过数值模拟验证了我们的提议，并在一个 8 量子比特分子汉密尔顿量的量子设备上进行了演示。通过利用具有几十个量子比特的量子设备，并借助高性能经典计算资源进行对角化，所提出的算法有可能解决一些具有挑战性的分子问题。
AllerTrans：使用深度学习
摘要：认识到蛋白质的潜在过敏性对于确保其安全性至关重要。过敏原是确定蛋白质安全性的主要问题，尤其是随着重组蛋白在新医疗产品中的使用越来越多。这些蛋白质需要仔细的过敏性评估以确保其安全性。但是，传统的实验室测试过敏既昂贵且耗时。为了应对这一挑战，生物信息学为预测蛋白质过敏性提供了有效且具有成本效益的替代方法。在这项研究中，我们开发了一种增强的深度学习模型，以基于其主要结构为蛋白质序列的主要结构来预测蛋白质的潜在过敏性。我们的方法利用了两个蛋白质语言模型，为每个序列提取不同的特征向量，然后将其输入到深层神经网络模型中进行分类。每个特征向量代表蛋白质序列的特定方面，并将它们组合起来可以增强最终结果，并平衡模型的灵敏度和特异性。该模型将蛋白质分类为过敏反应或非过敏性类别。我们提出的模型表明，与ALGPRED 2.0模型相比，所有评估指标的可接受改进，其敏感性为97.91％，特异性为97.69％，精度为97.80％，使用Algpred 2.0 2.0 Dataaset的ROC曲线在99％下的敏感性为97.80％，使用标准的五fordation fortal-forcectation。