XiaoMi-AI文件搜索系统
World File Search System连接映射技术不反映大脑中的功能梯度
功能梯度,其中响应特性在大脑区域逐渐变化,作为大脑的关键组织原理。使用静止状态和自然观看范式的最新研究表明,这些梯度可以通过“连接映射”分析从功能连接模式重建。然而,局部连接模式可能会被数据分析期间的空间自相关所混淆,例如,通过坐标空间之间的空间平滑或插值。在这里,我们研究了这种混杂是否可以产生虚幻的连接梯度。我们生成了包含受试者功能体积空间中随机白噪声的数据集,然后选择使用空间平滑和/或将数据插入到不同的体积或表面空间中。平滑和插值引起的空间自相关能力用于连接映射,以在许多大脑区域产生体积和表面的局部梯度。此外,这些梯度似乎与从真实自然观看数据中获得的梯度高度相似,尽管在某些情况下从真实数据和随机数据产生的梯度在统计上是不同的。我们还重建了整个脑的全球梯度 - 尽管这些梯度似乎不太容易受到人工空间自相关的影响,但再现先前报道的梯度的能力与分析管道的特定特征紧密相关。这些发现意味着需要谨慎解释连接梯度。这些结果表明,先前报道的连接映射技术鉴定出的梯度可能会被分析期间引入的人工空间自相关所混淆,在某些情况下,在不同的分析管道中可能会繁殖很差。
为什么具有不完整市场的开放经济模型的全球和本地解决方案有所不同,以及为什么它重要
4我们使用Mendoza和Villalvazo(2020)开发的FIPIT算法。该算法修改了欧拉元素方程式的标准迭代方法,以避免求解同时求解非线性方程(如标准时间迭代方法)和不规则的插值(如内源性网格方法)。进行比较,附录B.1.2使用值函数迭代解决了模型。5在De Groot等人的附录B.3.7中。(2019年),我们提出了三阶应用程序(3OA)结果,并发现除非引入随机波动率,否则3OA是不必要的(请参阅De Groot,2016年)。对于QLOBC,我们使用DynareObc算法。div> dynareObc和oxcbin时,当均衡是唯一的时候,可以提供相同的解决方案。dynareObc的优点是它在有限的时间内收敛,并且可以测试平衡多重性。6在De Groot等人中。 (2019年),我们研究了针对的校准设置以匹配NFA的第一阶自相关。 我们发现的定性特征没有变化。6在De Groot等人中。(2019年),我们研究了针对的校准设置以匹配NFA的第一阶自相关。我们发现的定性特征没有变化。
B.Tech第四学期
模块1:线性代数简介(8个讲座)向量,向量空间,线性独立性,碱基和维度,正交性,线性图和矩阵,矩阵的基本子空间,rank-nullity Theorem。模块2:光谱分解(6个讲座)特征值,不变子空间,内部产物,规范,正统碱基,光谱定理,等法,极值和奇异值分解,应用。模块3:矩阵(5个讲座)特殊矩阵,规范和决定因素的特性。模块4:概率简介(6个讲座)经典和公理概率,概率空间,条件概率和独立性,总概率,贝叶斯规则。模块5:随机变量(8个讲座)定义,常见示例,累积分布函数,概率质量函数,概率密度函数;随机变量的函数;期望 - 卑鄙,差异和时刻;特征和瞬间的功能;特殊的随机变量 - 二项式,泊松,统一,指数和高斯;共同时刻,有条件的期望;协方差和相关性 - 独立,不相关和正交随机变量;两个随机变量的函数;大量法律和中央限制定理的法律薄弱。模块6:随机过程简介(3个讲座)离散和连续时间过程;随机过程的概率结构;卑鄙,自相关和自相关功能;随机过程的示例:白噪声。文本/参考书:
B.Tech Power电子和仪器
模块1:线性代数简介(8个讲座)向量,向量空间,线性独立性,碱基和维度,正交性,线性图和矩阵,矩阵的基本子空间,rank-nullity Theorem。模块2:光谱分解(6个讲座)特征值,不变子空间,内部产物,规范,正统碱基,光谱定理,等法,极值和奇异值分解,应用。模块3:矩阵(5个讲座)特殊矩阵,规范和决定因素的特性。模块4:概率简介(6个讲座)经典和公理概率,概率空间,条件概率和独立性,总概率,贝叶斯规则。模块5:随机变量(8个讲座)定义,常见示例,累积分布函数,概率质量函数,概率密度函数;随机变量的函数;期望 - 卑鄙,差异和时刻;特征和瞬间的功能;特殊的随机变量 - 二项式,泊松,统一,指数和高斯;共同时刻,有条件的期望;协方差和相关性 - 独立,不相关和正交随机变量;两个随机变量的函数;大量法律和中央限制定理的法律薄弱。模块6:随机过程简介(3个讲座)离散和连续时间过程;随机过程的概率结构;卑鄙,自相关和自相关功能;随机过程的示例:白噪声。文本/参考书:
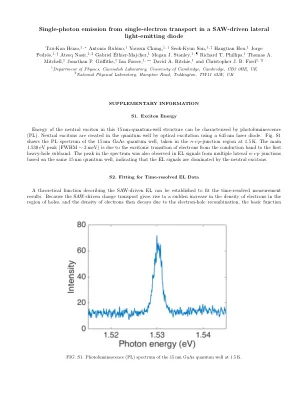
SAW驱动横向发光二极管中单电子传输的单光子发射
h(t) 可以理解为来自 SAW 最小值的 EL 信号。因此,自相关直方图可以看作是一系列等距函数 J(∆t)=(h∗hmirror)(∆t) 的总和。图 S4(a) 显示了 τ = 0.2 和 w = 0.05 的 h(t) 的示例,而图 S4(b) 显示了镜像 hmirror(t)。它们的卷积 J(∆t) 绘制在图 S4(c) 中。这个单峰可以理解为图 S3 中各个峰的实际形状,这意味着即使这些峰之间存在明显的重叠,也可以单独评估特定峰的贡献。因此,如果已知 SAW 驱动的 EL 的理论函数 J(∆t),就可以更准确地估计来自抑制峰的真实信号,例如图 3(a) 中的抑制峰。从图 3(b) 中平均直方图的拟合结果可以看出,每个峰的形状由 J (∆ t ) 确定,其中 τ = 99.6 ps,w = 33 ps,BG g2 = 2.79。可以假设图 3(a) 中的每个峰具有相同的形状,但由于统计样本方差,其峰幅度不同。这些在 ∆ t = ∆ t (i) 处的峰具有不同的幅度 A g2(i) ,其与 g (2) (∆ t (i) ) 成正比。反映方差的改进自相关函数可以表示为
时间分辨 Hanbury Brown–Twiss 干涉测量法...
双光子频率梳 (BFC) 是用于大规模和高维量子信息和网络系统的有前途的量子源。在这种情况下,单个频率箱的光谱纯度对于实现量子网络协议(如隐形传态和纠缠交换)至关重要。测量组成 BFC 的未预告信号或闲置光子的时间自相关函数是表征其光谱纯度并进而验证双光子状态对网络协议的实用性的关键工具。然而,通过实验可获得的测量 BFC 相关函数的精度通常受到探测器抖动的严重限制。结果,相关函数中的精细时间特征(不仅在量子信息中具有实用价值,而且在量子光学研究中也具有根本意义)丢失了。我们提出了一种通过电光相位调制来规避这一挑战的方案,通过实验证明了集成 40.5 GHz Si 3 N 4 微环产生的 BFC 的时间分辨 Hanbury Brown-Twiss 特性,最高可达 3 × 3 维二四分体希尔伯特空间。通过使电光驱动频率从梳状的自由光谱范围略微失谐,我们的方法利用 Vernier 原理来放大时间特征,否则这些特征会被探测器抖动平均掉。我们在连续波和脉冲泵浦模式下展示了我们的方法,发现与理论高度一致。我们的方法不仅揭示了贡献频率箱的集体统计数据,还揭示了它们的时间形状 - 标准全积分自相关测量中丢失的特征。
京津冀可再生能源产业特征及空间集聚关联性
摘要:京津冀是我国重点发展区域,可再生能源产业尤受关注。本文旨在将空间信息与可再生能源产业相结合,揭示产业时空演变特征及其驱动因素。研究发现,京津冀产业表现出明显的集聚格局,京津冀区域可再生能源产业2005—2010年Moran’s I=0.385579,2010—2015年Moran’s I=0.319463,2015—2020年Moran’s I=0.329409。全局空间自相关分析显示,京津冀区域可再生能源产业集聚水平并未提高,但局部空间自相关显示,交通运输和商业水平较高的区域在空间上趋于显著集聚。通过Moran指数发现京津冀产业呈现出明显的集聚格局,通过热点分析发现产业集聚主要发生在北京、天津、石家庄和张家口,这可以用城市化带来的要素集聚效应来解释。但进一步计算区位商、赫尔曼系数和基尼系数,发现京津冀地区存在明显的区域差异,如单极集聚效应在减弱。进一步的三相空间椭圆更形象地揭示了京津冀地区可再生能源产业在过去20年中持续形成的良性产业扩张。产业从首都北京起步,向西南转移,带动了河北、天津等地可再生能源产业发展,促进了京津冀经济圈协同发展。
研究激光诱导的损伤和相关的多光子吸收变化,以高重复速率的niobate晶体变化飞秒泵
图2 LIDT测量的实验设置:λ /2-半波长相板,p-偏振器,w-楔子,l-镜头,镜头,pm -power仪。在这里:红色箭头 - 泵辐射(1.03 µm),绿色箭头 - 泵的第二个谐波(0.515 µm); b)YB的自相关轨迹:kgw(Pharos)辐射,通过自相关器(GECO,Light Conversion Co,Ltd)和C)571 kHz和298 fs的LIDT测量测量(P OUT-输出功率,P IN- IN -ID IND -ID型泵送功率)。
HyperRapid NXT 266
注释:1. 由于我们持续进行产品改进计划,规格如有变更,恕不另行通知。2. 所有规格均为 800 kHz 规格。3. 预热时间后,冷却器温度 = 23 +/- 0.1°C 4. 最大传输率下,可变衰减器和过程快门的最大功率。5. 800 kHz 操作下的 DUV 自相关。6. 超过 8 小时,±1°C 环境温度。7. 单脉冲操作(突发数 = 1)。8. 稳定状态(无脉冲选通或脉冲重复率变化)。9. M x 2 和 M y 2 的平均值。