机构名称:
¥ 1.0
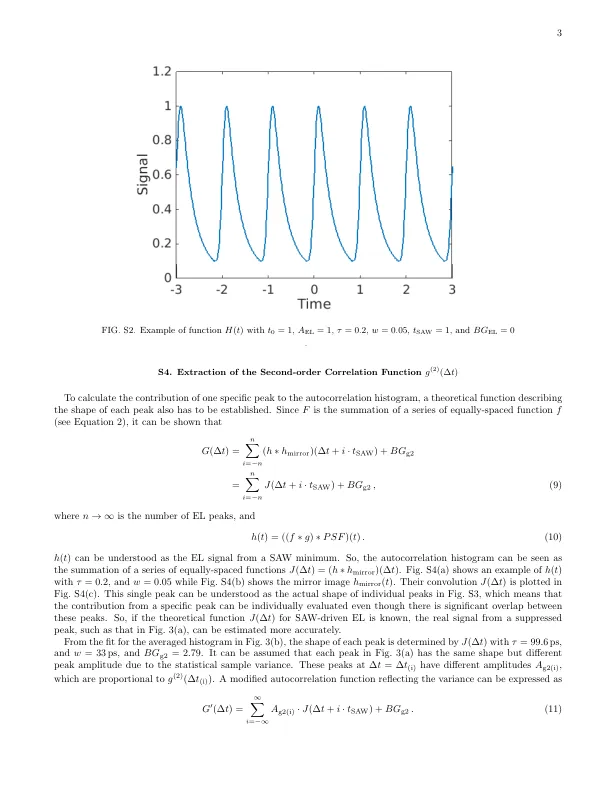
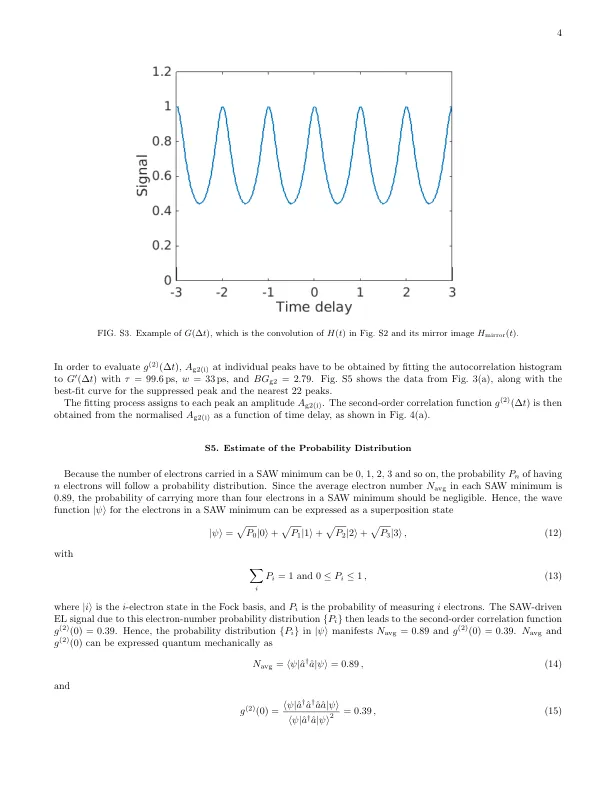
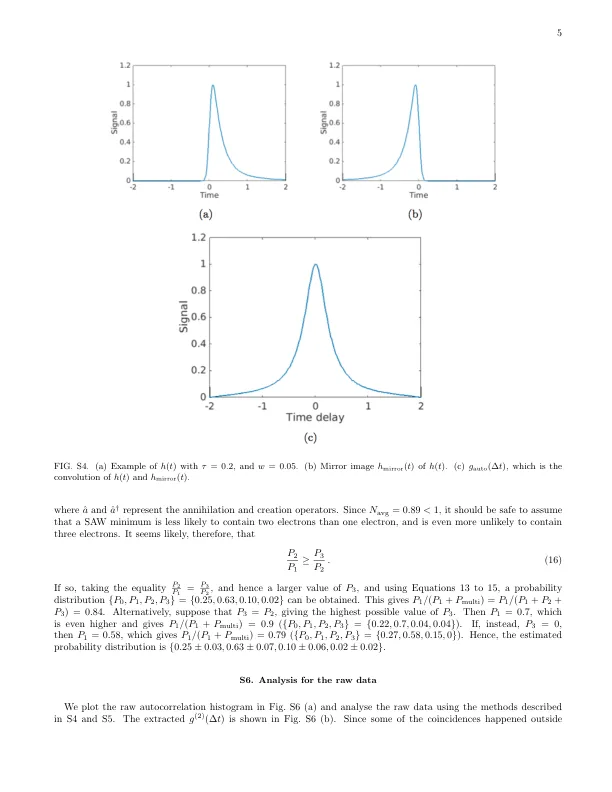
h(t) 可以理解为来自 SAW 最小值的 EL 信号。因此,自相关直方图可以看作是一系列等距函数 J(∆t)=(h∗hmirror)(∆t) 的总和。图 S4(a) 显示了 τ = 0.2 和 w = 0.05 的 h(t) 的示例,而图 S4(b) 显示了镜像 hmirror(t)。它们的卷积 J(∆t) 绘制在图 S4(c) 中。这个单峰可以理解为图 S3 中各个峰的实际形状,这意味着即使这些峰之间存在明显的重叠,也可以单独评估特定峰的贡献。因此,如果已知 SAW 驱动的 EL 的理论函数 J(∆t),就可以更准确地估计来自抑制峰的真实信号,例如图 3(a) 中的抑制峰。从图 3(b) 中平均直方图的拟合结果可以看出,每个峰的形状由 J (∆ t ) 确定,其中 τ = 99.6 ps,w = 33 ps,BG g2 = 2.79。可以假设图 3(a) 中的每个峰具有相同的形状,但由于统计样本方差,其峰幅度不同。这些在 ∆ t = ∆ t (i) 处的峰具有不同的幅度 A g2(i) ,其与 g (2) (∆ t (i) ) 成正比。反映方差的改进自相关函数可以表示为
SAW驱动横向发光二极管中单电子传输的单光子发射
主要关键词