XiaoMi-AI文件搜索系统
World File Search SystemFET通道中的电子散射效应-IUE
有关能量分布函数(EDF)的准确知识对于建模半导管设备中热载体损伤的形成至关重要[1]。电子 - 电子散射(EES)可以实质上影响EDF [2-4],并且必须正确地包括在运输模型中。在EES存在下变为非线性的Boltzmann方程的解决方案方法是基于确定性的迭代方法[2]或集合Monte Carlo方法[5-7]。 在这项工作中,我们求助于两个粒子动力学方程,该方程在粒子间相互作用的情况下也保持线性。 该方程溶液的蒙特卡洛算法基于轨迹对的计算和策略。 两个波向量𝐤1和𝐤2被同时考虑,这意味着该方法实际上是在对六维动量空间进行采样。 然而,将Momentum空间的维度加倍,不会降低Monte Carlo方法的效率,因为它与确定性方法形成鲜明对比,因此它不会遭受维度的诅咒。解决方案方法是基于确定性的迭代方法[2]或集合Monte Carlo方法[5-7]。在这项工作中,我们求助于两个粒子动力学方程,该方程在粒子间相互作用的情况下也保持线性。蒙特卡洛算法基于轨迹对的计算和策略。两个波向量𝐤1和𝐤2被同时考虑,这意味着该方法实际上是在对六维动量空间进行采样。将Momentum空间的维度加倍,不会降低Monte Carlo方法的效率,因为它与确定性方法形成鲜明对比,因此它不会遭受维度的诅咒。
破解市场奥秘的代码-ClickedTools
市场本质上是混乱的,受无数因素的影响,从地缘政治紧张局势到自然灾害。算法如何导航这种不确定性?他们通过拥抱不可预测性来做到这一点。蒙特卡洛模拟:算法模拟了数千种潜在的未来市场情况,为广泛的结果做准备。自适应学习:使用增强学习,算法不断地完善其策略来响应市场变化,就像他们从经验中学习一样。黑天鹅的准备:一些算法专门识别罕见的高影响事件(“黑天鹅”),并制定了利用它们的策略。
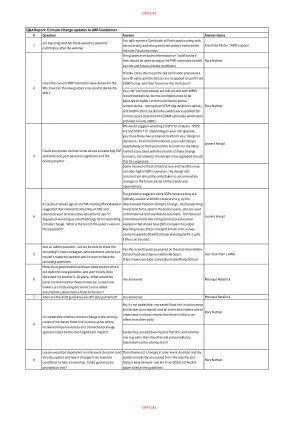
问答报告:气候变化更新到ARR指南
新指南包括有关新指南输入中不确定性的信息(例如,每个变暖度的降雨深度缩放因子),按置信区间表示。该指南还包括有关与未来气候预测相关的较高“认知”不确定性的注释。作为大坝所有者特别是使用更严格的风险评估工具(例如USACE TotalRisk),它不仅可以使用“最佳估计”洪水频率曲线,因此能够将这些不确定性包括在蒙特卡洛采样和派生频率曲线中是有益的。是否有可用于这些输入的经验分布,以允许(例如)每次变暖程度的降雨深度增加(例如)?
通过算法量子退火对各种近乎最佳的解决方案采样
在许多科学的学科和应用中(例如人工智能和运营研究)中,对硬优化问题进行采样一组高质量的解决方案具有很大的实践相关性。主要的开放问题之一是基于蒙特卡洛技术的典型随机求解器缺乏恐怖性或模式崩溃,导致概括或缺乏对不确定性的鲁棒性。当前,尚无通用度量标准来量化各种求解器的性能缺陷。在这里,我们引入了一种新的多样性度量,用于量化NP-HARD优化问题的独立近似解决方案的数量。除其他外,它允许通过所需的多样性(TTD)进行基准测试求解器的性能,这是经常使用的时间到达(TTS)的概括。我们通过比较各种量子退火策略的采样能力来说明该指标。特别是,我们表明,不均匀的量子退火时间表可以通过控制时空分离的临界界面来重新分配和抑制拓扑缺陷的出现,从而使相对于TTS和TTD都具有优势,从而使得与标准量子退火计划相比,与TTD相对于TTD,以寻找稀有解决方案。使用路径综合蒙特卡洛模拟可用于多达1600吨,我们证明,在有效的近似张量张量网络收缩的指导下,量子波动的量子驱动驱动可以显着减少与本地场随机挫败的2D旋转镜的硬性局部性的比例。具体来说,我们观察到,通过创建一类算法量子相变,可以通过减少25%以上的难度样本实例的比例来增强溶液的多样性。
arxiv:2401.01629v1 [cs.lg] 2024年1月3日
用于描述分布,而概率质量函数(PMF)用于离散数据。当综合数据时,可以通过从现有数据的分布中进行采样来生成新的数据点。插值和外推。插值和诱惑涉及在现有数据点之间或之外生成新的数据点。这对于时间序列,地理数据等特别有用。一种常见的插值方法是线性插值,其中新点的值取决于两个已知点之间的线性关系。蒙特卡洛模拟。蒙特卡洛模拟启用随机抽样,以模拟真实系统中的不确定性。在数据综合中,该方法用于通过随机从已知的分布中进行随机采样来生成新样本。它在财务,工程和物理建模中找到了常见的应用。基于模型的采样。此方法涉及利用现有数据的统计模型来预测新的数据点。例如,可以将线性回归模型拟合到存在数据,并且可以通过随机采样模型参数来生成新的数据点。这种方法对于表现线性关系的数据特别有效。内核密度估计。 内核密度估计插入每个数据点周围放置核(通常是高斯内核)并计算每个点的贡献以估计概率密度函数。 这对于捕获数据分布的复杂性和多模式很有用。内核密度估计。内核密度估计插入每个数据点周围放置核(通常是高斯内核)并计算每个点的贡献以估计概率密度函数。这对于捕获数据分布的复杂性和多模式很有用。生成新样本时,可以根据估计的概率密度函数进行随机采样。
量子旋转的伪马约拉拉伪造功能重新归一化
我们实施了Honerkamp和Salmhofer [Phys。修订版b 64,184516(2001)]进入了量子自旋系统的伪摩霍拉纳功能重新归一化组方法。由于这种方法的重新归一化组参数是物理量,因此与更常规的重新归一化组参数相比,温度t,数值效率显着提高,尤其是在计算限制性 - 温度相图时。我们首先采用此方法来确定简单的立方晶格上J 1 -j 2 Heisenberg模型的有限温度相图,在此,我们的发现支持了围绕高挫折点J 2 = 0的消失的小型非磁相的主张。25 J 1。 也许最重要的是,我们发现温度流方案在检测有限的平移过渡方面是有利的。 最后,我们将温度流方案应用于方格上的偶极XXZ模型,在那里我们找到了具有较大非磁性状态的丰富相图,以至于最低的可访问温度。 在适用于错误控制的(量子)蒙特卡洛方法的比较时,我们发现了出色的定量一致性,与数值确切的结果相比偏差不到5%。25 J 1。也许最重要的是,我们发现温度流方案在检测有限的平移过渡方面是有利的。最后,我们将温度流方案应用于方格上的偶极XXZ模型,在那里我们找到了具有较大非磁性状态的丰富相图,以至于最低的可访问温度。在适用于错误控制的(量子)蒙特卡洛方法的比较时,我们发现了出色的定量一致性,与数值确切的结果相比偏差不到5%。
不确定性在湿度和模型参数中的影响对预测contail能量强迫的预测
抽象的先前工作表明,尽管飞机冷凝径(捕捞尾巴)对气候的净效应正在变暖,但每米cont虫的能量强迫的确切幅度仍然不确定。在本文中,我们探讨了拉格朗日概要模型(COCIP)在识别具有高尾尾能量强迫的战争段时的技能。我们发现,技能仅大于气候预测,甚至考虑了天气场和模型参数的不确定性。我们通过使用欧洲中等天气预报中心(ECMWF)的集合ERA5天气再分析来估计由于湿度而导致的不确定性,作为蒙特卡洛投入到cocip。我们通过迫使在巡航高度上进行的原位湿度测量值匹配匹配ERA5湿度数据的不偏见和纠正不分散。我们将使用一个集合成员之一计算出的Cocip能量强迫估计值作为地面真理的代理,并报告COCIP在识别具有较大正面代理能量强迫的细分市场方面的技能。我们通过使用与文献一致的不确定性分布中绘制的COCIP模型参数进行蒙特卡洛模拟,进一步估计COCIP中模型参数引起的不确定性。当cocip输出在季节中平均以形成气候预测时,预测代理的技能为44%,而cocip cocip输出的技能为84%。如果这些结果延续到了真实的(未知)的围栏EF,则表明能量强迫预测可以减少潜在的避免避免途径调整的数量2倍,从而减少避免避孕的成本和燃料的影响。
Vitae课程(2025年1月6日)
•W。Thompson等。“在二进制棕色矮人伴侣GL229 BA和BB的轨道上。”天文学期刊(接受),2025+。•S. Luu,Z。Xu,N。Surjanovic,M。Biron-Lattes,T。Campbell,A。Bouchard-cˆotˆe。“吉布斯采样速度比在GLM上的哈密顿蒙特卡洛更快吗?”国际人工智能与统计会议,2025年(接受)。•T。Campbell。 “贝叶斯核心质量的一般界限。”神经信息处理系统的进展,2024年(接受26%)。 •M. Biron-Lattes,T。Campbell,A。Bouchard-Cˆot´e。 “通过非可逆模拟回火自动仿真。”美国统计协会杂志(接受),2024年。 •N。Chen,T。Campbell。 “马尔可夫链蒙特卡洛。”国际人工智能与统计会议,2024年(27%接受)。 •M。Biron-Lattes*,N。Surjanovic*,S。Syed,T。Campbell,A。Bouchard-Cˆot´e。 “ Automala:本地自适应大都会调整后的Langevin算法。”国际人工智能与统计会议,2024年(27%接受)。 •G.C. Diluvi,B。Bloem-Reddy,T。Campbell。 “离散变量的混合变分流。”国际人工智能与统计会议,2024年(27%接受)。 •S. Winter,T。Campbell,L。Lin,S。Srivastava,D。Dunson。 “贝叶斯计算中的新兴方向。”统计科学39(1),62-89,2024。 •Z. Xu,T。Campbell。•T。Campbell。“贝叶斯核心质量的一般界限。”神经信息处理系统的进展,2024年(接受26%)。•M. Biron-Lattes,T。Campbell,A。Bouchard-Cˆot´e。“通过非可逆模拟回火自动仿真。”美国统计协会杂志(接受),2024年。•N。Chen,T。Campbell。“马尔可夫链蒙特卡洛。”国际人工智能与统计会议,2024年(27%接受)。•M。Biron-Lattes*,N。Surjanovic*,S。Syed,T。Campbell,A。Bouchard-Cˆot´e。“ Automala:本地自适应大都会调整后的Langevin算法。”国际人工智能与统计会议,2024年(27%接受)。•G.C.Diluvi,B。Bloem-Reddy,T。Campbell。“离散变量的混合变分流。”国际人工智能与统计会议,2024年(27%接受)。•S. Winter,T。Campbell,L。Lin,S。Srivastava,D。Dunson。“贝叶斯计算中的新兴方向。”统计科学39(1),62-89,2024。•Z. Xu,T。Campbell。“拥抱混乱:分析和诊断变异流中数值不稳定性。”神经信息处理系统的进步,2023年(接受26%)。
损伤容限航空航天结构失效概率估计
3.1.1 单次飞行失败概率 ............22 3.1.2 裂纹检测概率 ..............24 3.1.3 等效初始缺陷尺寸 ..............25 3.1.4 每次飞行的最大施加应力 ...........28 3.1.5 检测概率曲线 .............30 3.2 PROF 软件 .。。。。。。。。。。。。。。。。。。。。。。。。.31 3.2.1 PROF 软件方法 .............31 3.2.2 PROF 示例问题 ................34 3.3 显式蒙特卡洛方法 ................40 3.3.1 分析例程 .................。。。。。。。40 3.3.2 蒙特卡罗程序的 SFPOF 和 PCD 估计 43 3.3.3 重要性抽样修改 ......44 3.3.4 CP4、CP6、CP7 和 CP7ext 的蒙特卡罗结果 ..45
微观交通模型,事故和保险损失
摘要该论文开发了一种方法,以使运输系统的微观模型可以访问统计研究。我们的方法不仅允许对历史损失的理解,而且还允许对可能发生的未来系统发生的事件进行理解。通过这样的反事实分析,从保险,也可以从工程学的角度来评估车辆和运输系统设计的变化对道路安全和功能的影响。在结构上,我们将总损耗分布近似为平均值混合物。这还产生了可以使用的估值程序,而不是蒙特卡洛模拟。特别是,我们基于开源式模拟器Sumo构建实现,并说明了反事实案例研究中该方法的潜力。




![arxiv:2401.01629v1 [cs.lg] 2024年1月3日](/simg/1\1904bc517d8e8e8c1dd7feb32aa47246b6aebc73.webp)




