机构名称:
¥ 1.0
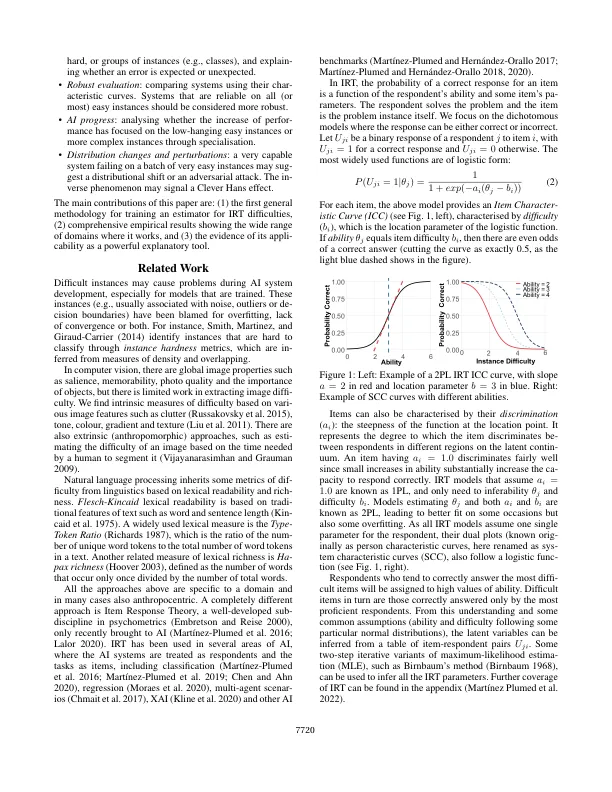
等式 1 的群体性质在 AI 的许多领域都很方便,因为我们在选择要部署的系统之前通常会应用各种技术。所有这些被丢弃的次优系统都可以重新用于计算难度,正如我们将在本文中看到的那样。然而,使用系统群体也会带来一些风险。例如,如果群体包含一个不符合要求的系统(在简单实例上失败,在一些困难实例上成功),则可能导致非常不稳定的难度指标。如果我们只是计算一组系统对每个实例的平均误差作为难度的代理,可能会发生这种情况(Mart´ınez-Plumed 等人,2019 年)。几十年前提出了一种解决这个问题的方法,称为项目反应理论 (IRT),其中难度是从项目(实例)和受访者(系统)矩阵中推断出来的,这使得符合要求的系统更具相关性。此外,IRT 给出了一个遵循正态分布的难度缩放指标,可以直接与系统的能力进行比较。然而,IRT 和其他难度指标都是从之前的性能结果中得出的,但不依赖于实例空间,因此我们无法预测新实例的难度。我们为这个重要问题提出了一个相对简单的解决方案:以问题特征作为输入、以难度作为输出来训练回归模型。本文涵盖了人工智能中的一系列问题,推导了它们的 IRT 难度,并为每个领域训练了一个回归模型——难度估算器,我们对其进行了系统性的评估。对于许多领域,根据 RMSE 和 Spearman 相关性,对 IRT 难度的估计非常好。我们在一系列应用上说明了这些难度模型的解释能力:
预测 IRT 难度的解释力
主要关键词