XiaoMi-AI文件搜索系统
World File Search SystemJHEP02(2025)173
过去二十年来,人们对量子信息理论的兴趣越来越浓厚,这是量子计算的基础,并向理论物理的各个分支进行了广泛的应用。尤其是,量子误差校正(QEC)是实现可容忍量子计算机与量子噪声(例如变形[1-5])的实验实现的关键。QEC代码是通过将量子状态(代码子空间)嵌入更大的希尔伯特空间来保护量子状态(代码子空间)免受错误的理论框架。在冷凝物理物理学中,构建了一大类QEC代码,以描述物质代码[6-8]和Fracton模型[9-12]等物质的拓扑阶段。另一方面,已经在高能理论中研究了全息代码[13-16],以了解一个较低维度的量子重力与量子场理论之间的全息二元性[17-19]。QEC代码已被利用来构建一组离散的二维形成共形场理论(CFTS),称为Narain Code CFT [20]。这概括了经典代码的手性CFT的结构[21],该代码长期很长时间[24,25]。narain代码CFT是骨CFT的,其光谱的特征是洛伦兹晶格与量子稳定器代码相关。Narain Code CFTS在模块化引导程序[26-28],搜索具有较大频谱差距的CFT [29,30]和全息
MATH1020-微积分和线性代数II-单位指南
单元描述Math1010中引入的线性代数和微积分的基础进一步探索和扩展。用代数涵盖的主题包括:反矩阵,决定因素,矢量空间和子空间,特征值以及特征向量以及线性变换。在微积分中,主题包括:限制,连续性和衍生物,数值集成,多项式,序列和序列和微分方程的进一步发展。另外,引入了两个或多个变量的复数和计算。学生在整个课程中都利用数学软件来支持和加强解决各种理论和实际问题的问题。
量子纠错码 - DR-NTU
信息是物理的。使用量子力学作为计算和信息处理的基础是明智的 [19]。在信息论、计算和物理学的交叉点上,数学家和计算机科学家必须从信息的量子物理实现的角度来思考。物理学家们经常就量子力学的性质和解释进行哲学辩论,现在转向利用其进行信息处理和测试理论的完整性。在不破坏内容的情况下,人们无法直接访问存储和处理在大量纠缠量子系统中的信息。将大规模量子计算变成现实极具挑战性。首先,它需要比传统系统中有效实现的技术复杂得多的误差控制技术。随着量子系统的尺寸和电路深度不断增加,误差控制变得越来越重要。量子误差控制是一组保护量子信息免受不必要的环境相互作用(称为退相干)影响的方法。经典方法是将携带信息的向量编码到更大的空间中,以便为错误检测和纠正提供足够的冗余。在量子设置中,信息存储在嵌入更大希尔伯特空间的子空间中,该子空间是复数 C 域上的有限维、范数向量空间。码字是量子态,错误是算符。好消息是,如果噪声可以保持在一定水平以下,它就不会成为弹性量子计算的障碍。这一重要见解是基于形成所谓阈值定理的开创性成果得出的。理论参考包括 Knill 等人在 [34] 中的阐述、Preskill 的工作
群、逻辑和计算 Brett Berger
摘要:对于域 F 上的有限维向量空间 V,令 P ( V ) 为 V 中按 ⊆ 包含排序的线性子空间集。我们证明,对于维数 V ≥ 3,射影空间 P ( V ) 经常(具有可定义参数)与 F 双向解释。这对于确定这些结构的一些逻辑性质有许多影响。这些性质包括 Th ( P ( V )) 和 Th ( F ) 的可判定性、P ( V ) 的一阶分类、P ( V ) 是否丰富(弱二阶逻辑等同于一阶逻辑)以及 P ( V ) 是否具有虚数的一致消去。
使用时间改进的 3D-QALAS 中的 T1 和 T2 映射...
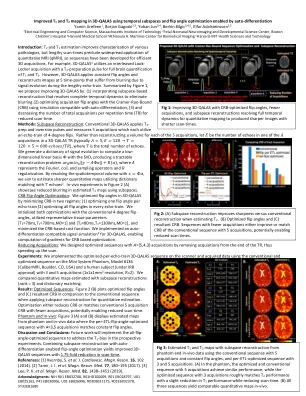
简介:T 2 和 T 1 估计可改善各种病理的特征描述,但较长的扫描时间阻碍了定量 MRI (qMRI) 的广泛应用,因此已经开发了序列以实现高效的 3D 采集。例如,3D-QALAS 1 利用交错的 Look-Locker 采集和 T 2 准备脉冲来对 T 1 和 T 2 进行全脑量化。但是,3D-QALAS 应用恒定翻转角并在 5 个时间点重建图像,这些时间点由于冗长的回波序列期间的信号演变而出现模糊。总结图 1,我们建议通过以下方式改进 3D-QALAS:(1) 结合基于子空间的重建来解决完整的时间动态以消除模糊 (2) 使用与自动微分兼容的模拟通过 Cramer-Rao 界限 (CRB) 优化采集翻转角,(3) 并减少每重复时间 (TR) 的总采集次数以缩短扫描时间。方法:子空间重建:传统 3D-QALAS 应用 T 2 准备和反转脉冲并测量 5 次采集,每次采集都利用 4 度翻转的回声序列。不是为 5 次采集中的每次采集重建一个体积,而是让 𝐸 成为 3D-QALAS TR 中 𝐴 采集之一中的回声数量(通常 𝐴= 5,𝐸= 120 →𝑇= 120 × 5 = 600 𝑒𝑐ℎ𝑜𝑒𝑠/𝑇𝑅 ),其中 𝑇 是回声总数。我们生成一个信号演化字典,用 SVD 计算低维线性基 Φ,从而产生一个易于处理的重建问题 𝑎𝑟𝑔𝑚𝑖𝑛 𝛼 ‖𝑦−𝐴Φ𝛼‖ + 𝑅(𝛼) ,其中 𝐴 表示傅里叶、线圈和采样算子以及 𝑅 正则化。通过使用 𝑥= Φ𝛼 解析时空体积,我们旨在利用与 𝑇 回声 2 的字典匹配来估计更清晰的定量图。图 2 (A) 中的体内实验表明,使用子空间可以减少估计的 T 2 图中的模糊。 CRB 翻转角优化:我们通过最小化两种方式的 CRB 来优化 3D-QALAS 中的翻转角:(1) 优化每个回波序列的一个翻转角 (2) 优化每个回波序列中的所有翻转角。我们使用传统的 4 度翻转角初始化了这两种优化,利用了代表性组织参数 [T 2 =70ms、T 1 =700ms、M0=1] 和 [T 2 =80ms、T 1 =1300ms、M0=1],并最小化了基于 CRB 的成本函数。我们为 3D-QALAS 实现了自动微分兼容信号模拟 3,从而能够计算基于 CRB 的优化的梯度。减少采集:我们通过从 TR 末尾移除采集,设计了具有 A ={5,4,3} 采集的优化序列,从而加快了扫描速度。实验:我们在扫描仪上实施了针对每个回波序列进行优化的 3D-QALAS 序列,并使用 Mini System Phantom、型号 #136(CaliberMRI,美国科罗拉多州博尔德)和人类受试者(经 IRB 批准)上的常规和优化序列采集数据,进行了 3 次和 5 次采集(1x1x1mm3 分辨率,R=2)。我们比较了使用子空间重建(秩 = 3)和字典匹配估计的定量图。结果:优化序列:图 2(B)绘制了优化的翻转角和(C)与应用子空间重建进行定量估计时的传统序列相比的所得 CRB。优化可以减少 CRB 或者以更少的采集次数匹配传统的 5 次采集 CRB,从而有可能缩短扫描时间。模型和体内:图 3(A)和(B)显示了从模型和体内数据估计的图,其中每个 ETL 翻转角优化的序列(A=3,5 次采集)与恒定翻转角匹配。讨论和结论:未来的工作将实施全翻转角优化序列来解决未来实验中的 T 1 偏差。将子空间重建与自动微分启用的翻转角优化相结合,可获得改进的 3D-QALAS 序列,并将扫描时间缩短 1.75 倍。参考文献:[1] Kvernby, S. et al. J. Cardiovasc. Magn. Reson. 16 , 102 (2014)。[2] Tamir, JI 等人 Magn. Reson. Med. 77 , 180–195 (2017)。[3] Lee, PK 等人 Magn. Reson. Med. 82 , 1438–1451 (2019)。致谢:NIH R01 EB032708、R01HD100009、R01 EB028797、U01 EB025162、P41 EB030006、U01 EB026996、R03EB031175、R01EB032378、5T32EB1680
m.tech-Aids-pg-syllabus-10.05.2024.pdf
数据科学教学的数学基础3 L小时每周的时间持续时间3小时请参见60 Marks CIE 40分数学分3课程目标:本课程的目的是1。讨论矢量空间和子空间。2。了解线性转换。3。探索随机过程。4。解释不同的估计。5。使用最小二乘近似值将曲线拟合到数据。课程成果:本课程完成后,学生将能够成功完成本课程,学生将能够:1。确定向量空间的基础和维度。2。计算线性转换的等级和无效。3。确定该过程的随机度量。4。推断统计参数的估计。5。将适当的模型应用于原始数据的回归诊断。
课程 | 物理和天文学
PHYS 764 - 量子信息 (3 学分) 量子信息理论和量子通信基础。主题包括:量子力学假设、经典信息和熵、经典信息压缩和经典典型集、量子熵和量子相对熵、量子态鉴别、舒马赫的量子压缩理论和量子典型子空间、使用量子信道传输经典信息、量子信道的经典容量定理。先决条件:MATH 344 或 MATH 544 或同等课程成绩为 C 或更高,或经讲师许可;MATH 511 或 STAT 511 或同等课程成绩为 C 或更高,或经讲师许可;无需量子力学知识。
arxiv:2302.12466v3 [Quant-ph] 2024年12月23日
带有门(局部单位)的量子电路尊重全球对称性,在量子信息科学及相关领域(例如凝结物质理论和量子热力学)中具有广泛的应用。,尽管它们广泛使用,但此类电路的基本属性并没有得到很好的理解。重新说,发现尊重全局对称性的通用单位也无法使用尊重相同对称性的门来实现,即使是大致也无法实现。这种观察提出了重要的开放问题:尊重全球对称性的K-local门可以实现哪些统一转换?换句话说,在全局对称性的主题中,相互作用的局部性如何限制复合系统的可能时间演变?在这项工作中,我们针对阿贝尔(交换性)对称的情况解决了这些问题,并开发了与这种对称性合成电路的建设性方法。非常明显的是,作为推论,我们发现,尽管相互作用的局部性仍然对可实现的单位施加其他限制,但在非亚伯式对称性的情况下观察到的某些限制并不适用于带有Abelian符号对称性的电路。例如,在具有一般非亚洲对称性的电路中,例如su(d),在一个子空间中实现的单一实现对称性的子空间中的一个不可还原表示(电荷)决定了多个其他分支机构中实现的单位者,具有对称对称性的不相等表示。此外,在某些部门中,而不是所有尊重对称性的单位,可实现的单位是该组的符号或正交亚组。我们证明,在阿贝尔对称性的情况下,这些限制均未出现。这个结果表明,在阿贝尔对称性下,全局非亚伯对称可能会以不可能的方式影响量子系统的热化。
一种用于指定自动化车辆操作设计域
摘要 - 该论文概述了一种系统的方法,可以为自动化车辆(AV)提供操作设计域(奇数)。该方法解决了各种传感器设置,广泛的操作领域属性以及各种驱动助手功能的复杂性,其特定法规会影响奇数。我们的方法论重点是识别和排除操作领域内的非安全区域。通过将操作域缩小到可管理的子空间,这种方法可以节省时间和精力在AV的测试过程中。作为概念证明,提出的方法已经通过一个实践示例验证,证明了其应用和可行性。索引术语 - 操作域,操作设计DO-主要,奇数规格,自动化车辆,传感器设置
在工作记忆任务期间,前额叶大脑活动的复发性神经网络模型
当将多个项目保存在短期内存中时,回顾性优先级优先级优先于另一个项目(复古示意)可以促进后续召回。然而,这种作用的神经和计算基础知之甚少。最近的一项研究记录了在复古任务期间猕猴侧向前额叶皮层(LPFC)中的神经信号,在(预先提示)和(会引发后)回归开始之前(预告症)和之后的延迟期间活动对比。他们报告说,在提示前延迟中,单个刺激被维持在神经种群活动的非独立子空间中,而在提示后延迟中,先前的项目被旋转成一个共同的子空间,有可能允许一种常见的读取机制。为了了解如何通过错误最小化可以学习此类代表性转变,我们通过监督训练了经常性的神经网络(RNN),以执行同等的提示回复任务。rnns提供了两个表示结合性颜色刺激的输入,然后进行了预示记忆延迟,位置返回和后提示延迟。我们发现,在猕猴LPFC中观察到的正交到平行的几何变换自然出现在经过训练以执行任务的RNN中。有趣的是,仅当需要在读数之前将提示信息用于几个周期的短期记忆中才能形成平行几何形状,这表明它在维护过程中可能具有鲁棒性。我们通过分析RNN的学习动态和连接模式以及用概率提示训练的模型的行为来扩展这些发现,从而使我们能够为将来的研究做出预测。总的来说,我们的发现与最新的理论说明是一致的,该账目提出的回顾将优先的内存项转化为前瞻性,面向动作的格式。







![arxiv:2302.12466v3 [Quant-ph] 2024年12月23日](/simg/8\80cdc4450f4f0aabe5903de7680c636e3a886838.webp)

