XiaoMi-AI文件搜索系统
World File Search SystemUB0100 AI 和 CV 计算引擎
锐化卷积 Chrome 生成数据类型转换中值可分离卷积色度去噪颜色类型转换颜色组合形态学操作查找表模糊边缘检测单应性卷积拉普拉斯哈里斯角最小最大调整大小下采样
原创文章 基于脑电图的情绪状态分类降维技术的比较分析
摘要:目的:本研究旨在评估各种降维方法(包括主成分分析 (PCA)、拉普拉斯评分和卡方特征选择)对脑电图 (EEG) 数据集分类性能的影响。方法:我们应用了降维技术,包括 PCA、拉普拉斯评分和卡方特征选择,并使用线性回归、K 最近邻 (KNN) 和朴素贝叶斯分类器评估了它们对 EEG 数据分类性能的影响。对模型的分类准确性和计算效率进行了评估。结果:我们的研究结果表明,所有降维策略通常都能提高或保持分类准确性,同时减少计算负荷。值得注意的是,PCA 和 Autofeat 技术可提高模型的准确性。结论:使用降维技术可以通过减少计算需求而不影响准确性来增强 EEG 数据分类。这些结果表明,这些技术有可能应用于既需要计算效率又需要高精度的场景。本研究中使用的代码可在https://github.com/movahedso/Emotion-analysis找到。
统计中的张量方法
3 Generalized Cumulants 61 3.1 Introduction and definitions 61 3.2 The fundamental identity for generalized cumulants 62 3.3 Cumulants of homogeneous polynomials 64 3.4 Polynomial transformations 65 3.5 Complementary set partitions 68 3.5.1 Equivalence classes 68 3.5.2 Symbolic computation 69 3.6 Elementary lattice theory 70 3.6.1 Generalities 70 3.6.2分区晶格的m obius功能72 3.6.3包含 - 排斥和二进制晶格74 3.6.4累积和分区晶格75 3.6.5累积的进一步关系77 3.7一些示例77 3.7一些涉及线性模型80 3.8累积空间82 3.9 Gaussian Momments 82 Rysents 85 3.9.19.1.1 issers85。拉普拉斯近似88 3.10.1两人分期膨胀88 3.10.2正式拉普拉斯扩张89 3.11书目注释90 3.12进一步的结果和练习3 92
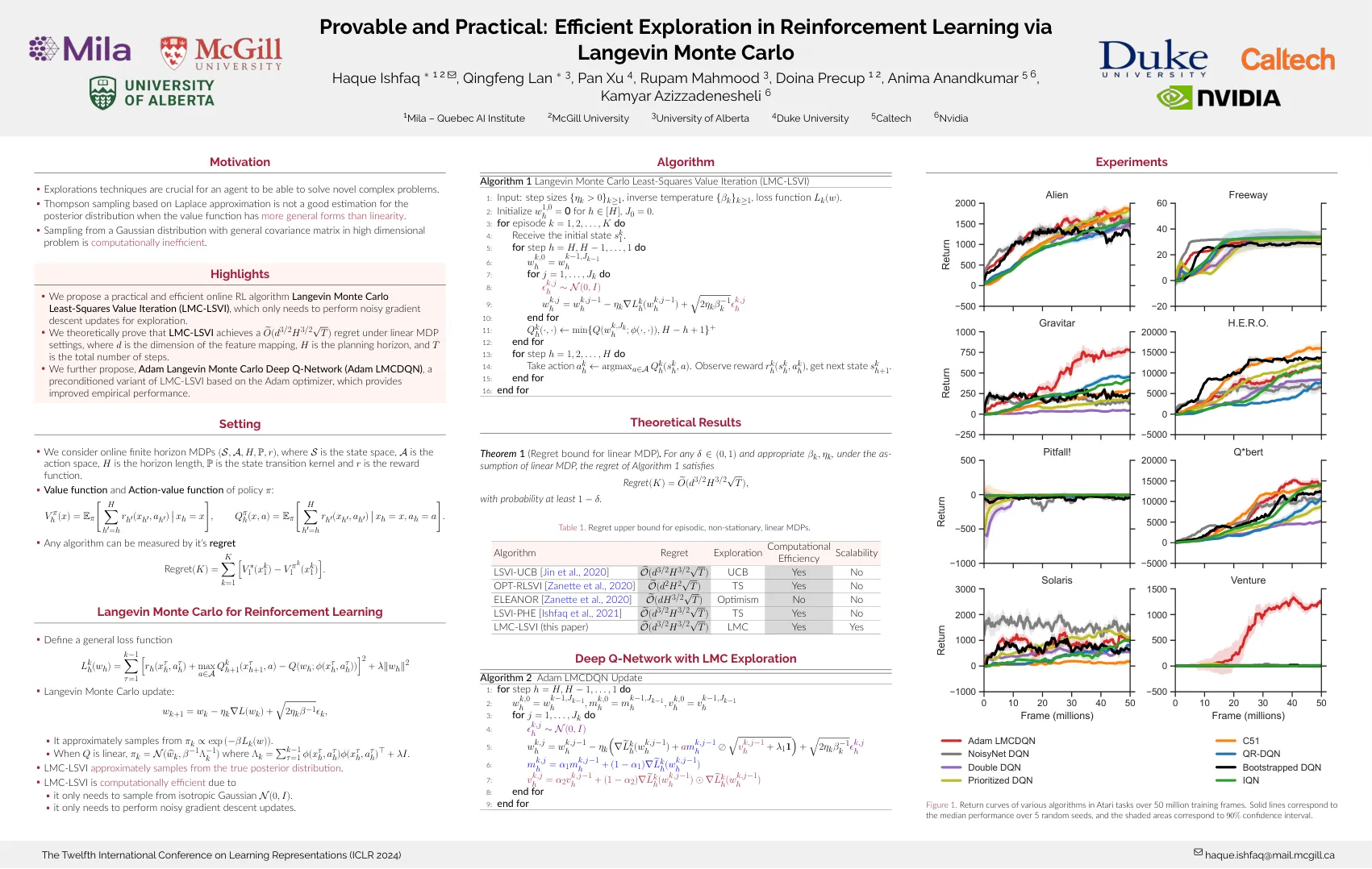
可证明且实用的:通过Langevin Monte Carlo
探索技术对于能够解决新的复杂问题的代理至关重要。基于拉普拉斯近似的汤普森采样是当值函数比线性更一般形式时,对后验分布不是一个很好的估计。在高维问题中具有一般协方差矩阵的高斯分布的采样在计算上效率低下。
已发布版本的引用 (APA):Apers, S., & de Wolf, R. (2020)。图稀疏化、切割近似和拉普拉斯算子求解器的量子加速
图稀疏化是大量算法的基础,从切割问题的近似算法到图拉普拉斯算子的线性系统求解器。在其最强形式中,“谱稀疏化”将边数减少到节点数的近似线性,同时近似地保留图的切割和谱结构。在这项工作中,我们展示了谱稀疏化及其许多应用的多项式量子加速。具体而言,我们给出了一种量子算法,给定一个具有 n 个节点和 m 条边的加权图,在亚线性时间内输出 ϵ -谱稀疏器的经典描述 e O ( √ mn/ϵ )。这与最佳经典复杂度 e O ( m ) 形成对比。我们还证明我们的量子算法在多对数因子范围内是最优的。该算法建立在一系列关于稀疏化、图扩展器、最短路径量子算法和 k 向独立随机字符串的有效构造方面的现有成果之上。我们的算法意味着解决拉普拉斯系统和近似一系列切割问题(例如最小切割和最稀疏切割)的量子加速。
关于对比学习的有限样本可识别性——......
▶ 我们遵循 [Hyvarinen et al., 2019] 中的设置。 ▶ si 是高斯变量和拉普拉斯变量的乘积。 ▶ u 对应不同的时间框架。 ▶ g ( · ) 是具有泄漏 ReLU 的神经网络。 ▶ h ( · ) , ϕ i ( · ) 采用具有 R 个神经元的 3 隐藏层网络建模。 ▶ 度量:si 和 hj ( x ) 之间的互信息。
使用跳投的生成建模
基于得分的扩散模型使用时间转移的扩散过程从未知目标分布中生成样品。这种模型代表了工业应用中的最新方法,例如人造图像产生,但最近注意到,通过考虑具有重尾部特征的注入噪声,可以进一步提高其性能。在这里,我将生成扩散过程的概括性化为一类广泛的非高斯噪声过程。我考虑由标准高斯噪声驱动的前进过程,并以超级强制的泊松跳跃为代表有限的活动莱维过程。生成过程被证明由依赖跳跃幅度分布的广义分数函数控制。概率流ode和SDE配方都是使用基本技术努力得出的,并且用于从多元拉普拉斯分布中得出的跳跃振幅实现。非常重要的是,对于捕获重尾目标分布的问题,尽管没有任何重尾特性,但跳跃延伸拉普拉斯模型的表现就超过了由α-稳定噪声驱动的模型。该框架可以很容易地应用于其他跳跃统计数据,这些统计数据可以进一步改善标准扩散模型的性能。
Hydromechanical.pdf -zihao li
非常规地材料通常表现出多模式孔径分布。,我们为多孔介质开发了一个综合框架,该培养基表现出多孔的孔隙率尺度,使用混合理论饱和到一种或两种类型的流体。分别明确得出和识别了管理方程式和构成定律。从能量平衡方程中出现的有效应力𝝈'对于弹性和弹性变形都可以采用,在这种变形中,孔隙和饱和效果起着核心作用。提出的模型是一般的,从某种意义上说,它适用于未耦合的仿真和耦合模拟。使用拉普拉斯变换和数值拉普拉斯反转方法求解了未耦合流动模拟的场方程。通过可视化无量纲结果,我们可以在自然断裂的储层的耗尽过程中获得对不同阶段的定量见解。用于耦合流量和地球力学模拟,带状负载问题以及可变形3D储层问题中的两相流量说明了可塑性,多重孔隙率,孔隙率交换和毛细管压力对系统响应的影响。
Laplacian框架中的化学反应网络
研究化学反应的动力学以及特别是振荡反应的现象,导致人们认识到,可以从某个有向图的图理论特性(称为化学反应网络(CRN))的图理论特性中预测化学反应的许多动力学特性。在此图中,边缘表示化学物质的反应和顶点。与经典待遇相比,在这项工作中,我们严重依赖于最近开发的有导图拉普拉斯人的理论,以简化对CRN理论的所谓定义零系统的传统处理。我们表明,可以通过分析与系统相关的有向图拉普拉斯式来理解这些不同方程式这些多项式系统的许多动力学。除了更简洁的数学处理外,这还导致了更加强大的结果。尤其是(i)我们表明,我们的拉普拉斯(Laplacian)的表现零定理明显比传统的定理强,并且(ii)我们在所有(laplacian)降低零病例中得出了简单的平衡位点的简单方程。本文以一种方式编写,以使数学受众易于访问材料。特别是没有假定的化学或物理知识。