XiaoMi-AI文件搜索系统
World File Search System与认知的共同模型桥接生成网络
引言智能系统通过拥有良好的老式人工智能(即Gofai或“象征性”)推理和连接主义统计学学习(例如Hitzler等。2022);但是,如何整合两者尚无共识。较少的方法之一是将生成的AI模型和认知体系结构整合到单个混合系统中。对人类认知结构进行建模的主要候选者是认知的常见模型,以前是心灵的标准模型(Laird,Lebiere和Rosen-Bloom 2017),但是目前它缺乏使低级连接因素在认知水平上可以解释的方法。认知的通用模型(CMC)概述了人类认知如何在计算机上运作的说明,并通过大规模的神经科学数据进行了验证(Stocco等人。2021)。相比之下,大多数生成神经网络不受与生物学的对应关系的约束,而是采用务实的方法来产生不知知的输出。认知建模和人工智能具有不明显的目标,即一方面解释和预测人类和动物的行为,并解决问题并执行任务而没有人类指导。然而,认知模型可以从当前深度学习方法的整体中受益,因为生成网络解决的许多任务都是认知建模缺乏详细过程模型的任务,例如受到启示,想象力和自然语言处理。为
发展性认知神经科学
内部沟(IP)与数值处理有关。最近的一项研究报告说,IPS硫模式与儿童和成人的算术和象征性数量能力有关。在本研究中,我们评估了患有发育障碍障碍(DD)的儿童和通常患有儿童(TD)的儿童的数值能力与IPS沟沟模式之间的联系,从而扩展了以前的分析,考虑了其他沟通特征和后心sulcus(POC)。首先,我们确认了IPS和POC的纵向沟道稳定性。第二,与TD相比,我们发现左截面IP的比例较低,双侧双侧的双层IPS形状较高。第三,我们的分析表明,算术是数值处理的唯一方面,它与IPS硫模式显着相关(截面与未切片),并且这种关系特定于左半球。和最后的相关性分析的年龄和算术分析在没有左左IP的儿童中表明,尽管它们在数值能力上可能具有固有的劣势,但这些可能会随着年龄的增长而改善。因此,我们的结果表明,只有左IPS沟模式与数值能力和其他因素相关的数值能力有关。
对批判性推理的基准测试LLM
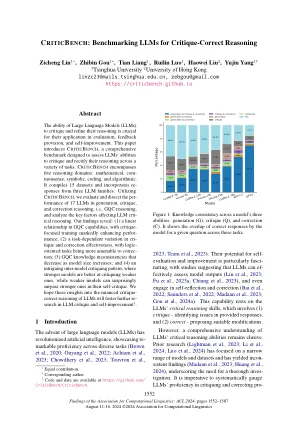
大语言模型(LLM)批评和完善推理的能力对于他们在评估,反馈提供和自我完善中的应用至关重要。本文介绍了C ritic B Ench,这是一个综合基准,旨在评估LLMS批评和纠正其跨各种任务的推理的能力。c ritic b ench包括五个推理领域:数学,commensense,象征性,编码和算法。它编译了15个数据集,并结合了来自三个LLM家族的重音。利用C ritic b ench,我们评估和剖析了17个LLM在生成,批评和校正推理中的表现,即GQC推理,并分析影响LLM批判性推理的关键因素。我们的发现揭示了:(1)GQC能力中的线性关系,以批判性的训练显着增强了表现; (2)依赖于任务和校正效率的任务变化,面向逻辑的任务更适合纠正; (3)随着模型大小增加而减小的GQC知识不一致; (4)一种有趣的模型间批判模式,在批评较弱的模型方面,更强大的模型更能更好,而较弱的模型可以超越其自我评价中的更强的模型。我们希望这些对LLM的细微批评的见解将进一步促进LLM批评和自我改善1。
基础模型时代的神经符号编程
Neuro-Symbolic编程(N E S Y),以应对培训神经网络的挑战,以解决复杂的推理任务,并带来了可解释性,可靠性和效率的额外好处。n e s y方法与象征性推理一起训练神经模型,但他们面临具有可伸缩性和训练的问题,这些问题将其限制在简单化的问题上。另一方面,纯净的神经基础模型现在可以通过提示而不是训练来达到最先进的表现,但是它们通常不可靠并且缺乏解释性。通过推理程序补充拟释放程序(我们称之为及时的符号符号(P r s y))提供了一种将这些模型用于复杂推理任务的方法。这样做提出了一个问题:神经符号在基础模型时代有什么作用?为了探讨这个问题,我们在计算,数据和程序方面重点介绍了N e s y的三个陷阱。然后,我们认为P r s y可以进行特定于任务的N e S y训练,从而为实现N e s y的最初目标提供机会而没有培训带来的缺陷。关键字:神经束,编程,基础模型,符号,培训
对图画书在儿童认知发展教育中的作用的分析
几个世纪以来,图画书一直是儿童文学中的主食,其最早的例子可以追溯到15世纪。这些书旨在通过单词和图片的结合吸引年轻的读者,以发展扫盲技能并促进认知发展。图画书是教幼儿新单词和概念以及为他们提供教育的重要工具。大量研究调查了阅读对父母和子女之间发展的关系的影响。最近发起了一项全新的研究系列,以调查儿童图画书的素质,这些素质鼓励学习和在更广阔的世界中进行教育的应用。儿童的象征性发展,类比推理和植根于幻想的思想可能会阻碍他们从图画书中检索信息的能力。之后,我们研究了关于图画书特征对儿童学习和转移科学概念,解决问题的技能,道德以及图画书中的单词和信件的影响的发展。在每个学习领域,我们研究了孩子的发展如何与书籍素质互动,以影响他们对知识的获取。我们得出的结论是,儿童从图画书中学习和转移知识的能力可能会受到某些书籍素质的阻碍,并且未来的研究应研究儿童发展能力与书籍特征之间的相互作用,以及他们如何影响他们的学习。
科学Matemate
拉格朗日力学的各种特征。实际上,众所周知,当且仅当相应作用的第一个变化具有固定极端物质时,曲线才能解决E-L。关于最小的通常,它持续了短时间。 实际上,由于可能存在共轭点,临界曲线不再最小化更大的时间。 仅在某些凸度假设下才有“最小化轨道”。 对于这种杰出而机械的相关类别的拉格朗日(Lagrangian) - 所谓的tonelli lagrangians- legendre变换是一种全球差异性和E-L方程,等于相应的汉密尔顿人的汉密尔顿方程。 对于自主系统,沿解决方案提供了保守的能量值。 除了拉格朗日式和哈密顿式设置之外,对动态相关的最小对象的搜索是现代动态系统理论的中心主题之一。 沿这个方向的第一个结果之一可以追溯到八十年代,其中所谓的单调扭曲图的所谓的奥布里·梅瑟理论。 该理论的一个重要应用是对数学台球的研究,从伯克霍夫(Birkhoff)到近期台球类型,如符号和外台球。 在二十年后,通过马瑟·曼尼(Mather-Mané)理论开发了这种理论从一种到更高程度的自由度的概括,在这种理论中,最小化措施而不是轨迹的措施起着至关重要的作用。 这种重要的理论从汉密尔顿 - 雅各比方程到象征性拓扑都有联系。该博士学位课程的目的是在自我包含的方式中呈现 - 在不同环境中的“最小行动原理”。通常,它持续了短时间。实际上,由于可能存在共轭点,临界曲线不再最小化更大的时间。仅在某些凸度假设下才有“最小化轨道”。对于这种杰出而机械的相关类别的拉格朗日(Lagrangian) - 所谓的tonelli lagrangians- legendre变换是一种全球差异性和E-L方程,等于相应的汉密尔顿人的汉密尔顿方程。对于自主系统,沿解决方案提供了保守的能量值。除了拉格朗日式和哈密顿式设置之外,对动态相关的最小对象的搜索是现代动态系统理论的中心主题之一。沿这个方向的第一个结果之一可以追溯到八十年代,其中所谓的单调扭曲图的所谓的奥布里·梅瑟理论。该理论的一个重要应用是对数学台球的研究,从伯克霍夫(Birkhoff)到近期台球类型,如符号和外台球。在二十年后,通过马瑟·曼尼(Mather-Mané)理论开发了这种理论从一种到更高程度的自由度的概括,在这种理论中,最小化措施而不是轨迹的措施起着至关重要的作用。这种重要的理论从汉密尔顿 - 雅各比方程到象征性拓扑都有联系。该博士学位课程的目的是在自我包含的方式中呈现 - 在不同环境中的“最小行动原理”。这一原则可以被视为一种自然动作的一种非常公认的“节俭”。
能源研究与社会科学-Fraunhofer -Publica
全自动车辆(最喜欢)可以改变基于私人汽车的移动性或“自动行动”,但最喜欢影响的方向是不确定的,并依赖于消费者。我们通过对加拿大不列颠哥伦比亚省的34个新车购买者进行半结构化访谈,调查消费者对最爱的反应及其与自动性的关系。首先,我们通过练习来评估消费者的反应,参与者设计他们的“理想下一辆车”,在最爱与常规车辆(CV)选项之间进行选择。我们发现,在有可能出售的最爱并包括方向盘的情况下,三分之二的参与者比CVS更喜欢最爱。第二,我们对成绩单数据进行定性内容分析,以调查消费者在访问私人拥有和共享最爱后使用自动化的参与。我们采用了消费者“自动化参与”的概念框架,考虑了对汽车拥有和住宅位置的偏好,汽车使用情绪,符号和社会观念以及社会规范。我们发现,少数参与者期望拥有更少的汽车或更改访问最爱后的住宅偏好。结果还表明,最喜欢的是,在很大程度上重现了汽车所有权的象征性和社会意义。与这些结果形成鲜明对比的是,几个特别的iPant期望最爱减少对整个社会的自动化影响。我们得出的结论是,采用最爱可以重现现有的消费者参与,并讨论对运输排放和政策的影响。
Sitnikova,M。A.等。 (2023)。低和高数学表演者中单词和数值格式的精确计算的神经相关性:fnirs stud
人们使用两个认知系统来理解和操作数字 - 非符号系统,主要依赖于无符号的幅度估计(例如,阿拉伯数字)和象征性系统,基于符号形式的数字处理(Ansari,2008; Feigenson,dehaene and dehaene and Spelke,dehaene and Spelke,2004; Waring and Pening and Penerner-wilger,2017)。数值认知的开发是一个逐步的过程,它是从非符号或近似数字系统开始的。近似数字系统是一个先天认知系统,它支持估计幅度的估计而不依赖语言或符号。然而,数量和基本算术技能的符号表示的作用随着年龄的增长而增加(Artemenko,2021)。基本的算术技能在日常生活,STEM教育以及许多涉及数学的科学中至关重要:在各种IT应用中,物理,化学,技术和工程学中都非常重要。更好地理解简单和复杂的精确计算的基本大脑机制对于数值认知非常重要,并深入了解了近似数字系统和精确符号表示系统中的网络中不同大脑区域之间的关系。实际上,将来可以使用这些知识来提高一个人的数字技能,消除与他们缺乏相关的问题(算术和数学素养的降低,dyscalculia)。已经表明,所有这些缺点都可能对整个经济和社会产生负面影响(Butterworth,Varma和Laurillard,2011年)。因此,实用
神经符号AI
摘要 - 主要由深神经网络驱动的人工intel-ligence(AI)的显着进步面临着围绕不可持续的计算传统,有限的鲁棒性和缺乏解释性的挑战。为了开发下一代认知AI系统,神经符号AI成为一种有希望的范式,融合了神经和象征性方法,以增强可解释性,鲁棒性和信任性,同时促进从较少数据的数据中促进学习。最近的神经符号系统在与推理和认知能力的协作人类方案中表现出了巨大的潜力。在本文中,我们旨在了解神经符号AI的工作量特征和潜在的架构。我们首先系统地对神经符号AI算法进行分类,然后通过实验评估和分析它们的运行时,记忆,计算运算符,稀疏性,稀疏性以及CPU,GPU和EDGE SOC的系统特征。我们的研究表明,由于矢量符号和逻辑操作的记忆性质,复杂的流量控制,数据依赖性,稀疏性变化以及有限的可伸缩性,神经符号模型的效率低下效率低下。基于分析见解,我们建议跨层优化解决方案,以提高神经符号计算的性能,效率和可扩展性。最后,我们从系统和建筑学的角度讨论了神经符号AI的挑战和未来方向。
更改了产品规则航空规则制定委员会...
此咨询通函(AC)提供了指导和一种全面的方法,可以根据《联邦法规法典》第14条(14 CFR)§450.115进行高保真飞行安全分析。根据第450.113(a)条的规定,需要进行飞行安全分析。AC 450.113-1(富达水平)提供了有关何时需要进行高保真飞行安全性分析以及如何确定所需忠诚度的指导。在需要高保真飞行安全分析的情况下,此AC 450.115-1为执行该分析的指导提供了符合§450.115(b)的指导。对于特定阶段或飞行的所有阶段,可能需要第450.115(b)条的高保真飞行安全分析。操作员的飞行安全分析方法必须说明所有可预见的事件以及在象征性和非社会化发射期间安全至关重要系统的失败,或者根据§450.115(a)可能会危及公共安全。根据第450.115(b)(1)条的规定,分析必须证明,公众的任何风险都符合第450.101节的安全标准,包括使用缓解,并考虑所有已知的不确定性来源,使用联邦航空管理局(FAA)接受的合规性手段(FAA)。分析必须在§§450.101(a)或450.101(b)中确定每种类型的公共风险的主要来源,以飞行阶段,危险来源(例如有毒曝光,惰性碎屑或爆炸性碎屑)和失败模式,以及符合第450.115(b)(b)(b)(2)。