机构名称:
¥ 1.0
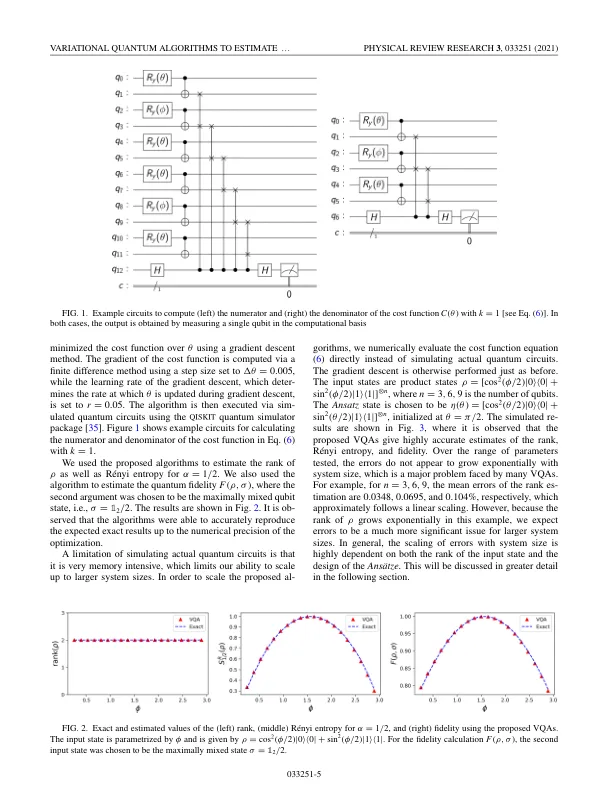
近年来,在一类早期量子计算设备中,人们越来越兴趣和快速发展,共同称为嘈杂的中间量子量子(NISQ)设备[1]。NISQ设备本质上是缺乏完整量子误差校正的量子计算硬件。由于缺乏误差校正,在此类设备上可用的门口和总相干时间受到限制。这意味着NISQ设备仅限于可以使用短深度量子电路执行的应用程序,超出该电路不可靠。虽然NISQ设备无法执行通用量子计算,但人们普遍期望它们能够在近期[2,3]中提供比古典计算机相对于经典计算机提供的魔鬼计算优势。开发适合NISQ设备的算法的一种方法是考虑杂交量子古典算法[4]。这样的算法试图通过将一部分计算的一部分向经典计算机铺开来降低整体量子电路深度要求。在其中,一种称为变分量子算法(VQA)的算法可以说是设计NISQ算法的最广泛使用和有希望的策略之一。在VQAS中,使用NISQ硬件进行经典计算的成本函数C(θ),而经典优化策略则用于发现最佳参数θ∗,以最大程度地减少成本函数。此类策略已用于诸如发现汉密尔顿人[5、6]的近似本征态的应用中,重新编译了量子电路[7],并解决了线性代数问题[8-10]。作为一类量子算法,VQAS
变异量子算法估计等级... -dr -ntu
主要关键词