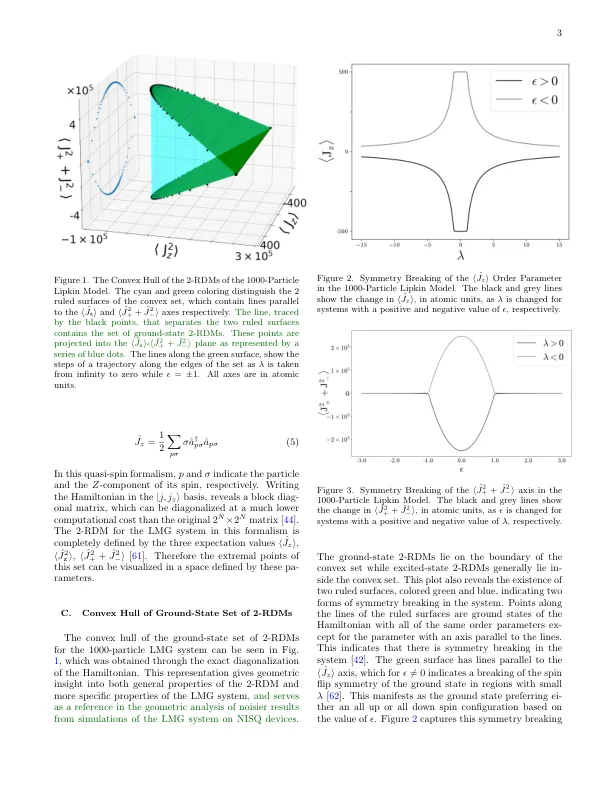
机构名称:
¥ 1.0
多粒子量子系统在绝对零度温度下不同相之间的转变称为量子相变,需要对粒子相关性进行精确处理。在这项工作中,我们提出了一种利用约化密度矩阵的几何结构来处理量子相变的通用量子计算方法。虽然典型的量子相变方法会检查序参数中的不连续性,但相变的起源——它们的序参数和对称性破坏——可以用两粒子约化密度矩阵 (2-RDM) 集的几何形式来理解。2-RDM 的凸集提供了量子系统的综合图,包括其不同相以及连接这些相的转变。由于 2-RDM 可以在量子计算机上以非指数成本计算,即使量子系统具有强相关性,它们也非常适合用于量子相变的量子计算方法。我们在 IBM 超导量子比特量子处理器上计算了 Lipkin-Meshkov-Glick 自旋模型的 2-RDM 凸集。尽管由于设备噪声,计算仅限于少数粒子模型,但与经典可解的 1000 粒子模型的比较表明,有限粒子量子解捕捉到了相变的关键特征,包括强相关性和对称性破坏。
使用...进行量子相变的量子模拟
主要关键词