机构名称:
¥ 1.0
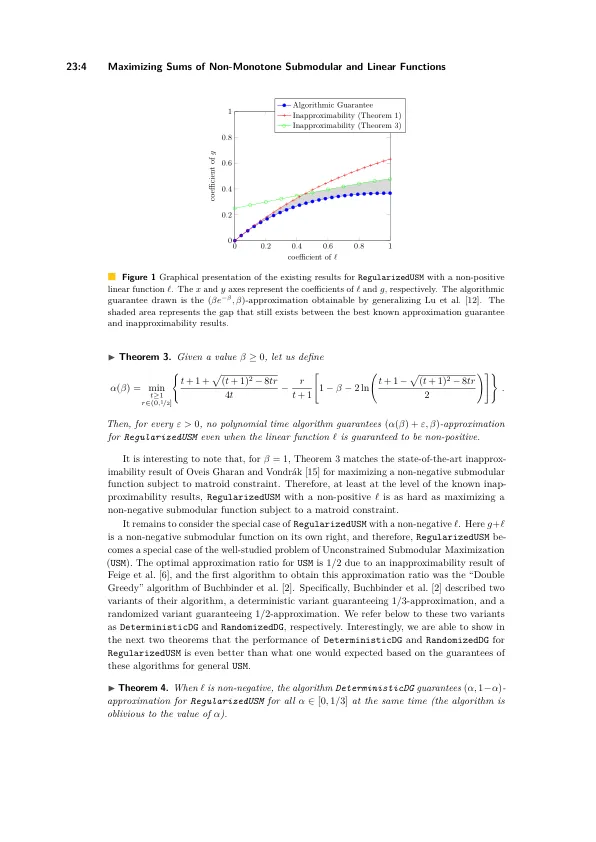
是出于实际应用的动机,最近的作品考虑了子模函数g和线性函数的总和的最大化。迄今为止,几乎所有此类工作仅研究了此问题的特殊情况,其中G也保证为单调。因此,在本文中,我们系统地研究了该问题的最简单版本,其中允许g是非单调的,即无约束的变体,我们将其称为正则不受约束的非约束下义最大化(正则化usizusm)。我们的主要算法结果是通用正则化usem的首个非平凡保证。对于线性函数ℓ是非阳性的正则uSM的特殊情况,我们证明了两个不Xibibibity的结果,表明先前的作品对这种情况暗示的算法结果远非最佳。最后,我们重新分析了已知的双重贪婪算法,以获得改进的正则化usemized use的特殊情况的保证,其中线性函数是非负的;我们通过表明无法获得(1 / 2,1)对这种情况的APPROXIMATION(尽管有直觉的论点表明这种近似保证是自然的)来补充这些保证。
最大化非单词酮子模型和线性函数的总和:了解无约束的情况
主要关键词