机构名称:
¥ 1.0
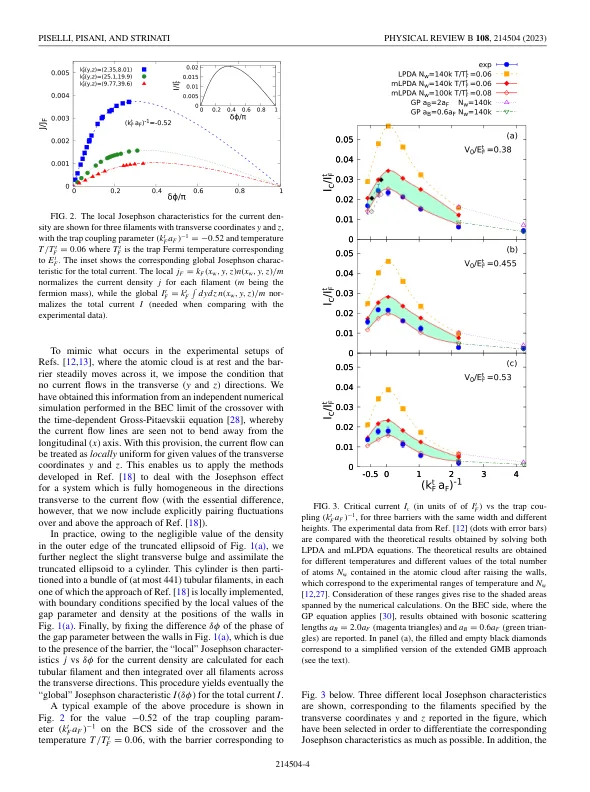
在有限温度下与嵌入非平凡的几何约束中的超低费米气体(通常是陷阱加屏障)中的超低费米气体对约瑟夫森效应的现实描述。在这里,我们应用了同伴论文中开发的理论方法[Pisani等。,物理。修订版b 108,214503(2023)],其中,在有限温度下,在BCS-螺旋 - 螺旋 - 内施坦 - 键酯(BEC)跨界的均值超出平均值之外,将其包括在有限温度下的交叉,与非trip虫的几何形状中的差距参数的详细描述结合在一起。以这种方式,我们能够解释约瑟夫森临界电流的实验结果,在低温下报告了整个BCS-BEC跨界的各种耦合以及在单位性时温度的函数。除了验证伴侣论文的理论方法外,我们的数值结果还揭示了约瑟夫森效应的通用特征,这些特征可能不会从对相应的实验的分析中出现,这些实验具有与超电气气体实验的独特固有功能,这是由于凝结的样品。
配对波动跨BCS-BEC跨界的作用
主要关键词