XiaoMi-AI文件搜索系统
World File Search System美国对基于技术的STEM教育研究的系统审查
2001年,美国科学发展协会(AAAS)发表了其两卷科学素养地图集,作为2061项目的一部分,该项目绘制了K – 12 Science课程。它包括主题,范围和序列,标准,基准,教学设计,培训,资源和评估[9]。这些卷突出了科学的动态性质及其与技术和数学的跨学科联系[9]。国家科学教育标准[10]和数学,以及学校数学的课程和评估标准,进一步支持了这些学科的整合[11]。专业协会建立的全国标准随后被提升为各州和地区。国家科学基金会教育和人力资源副总监贾迪思·拉马里(Judith Lamarie)创建了STEM首字母缩写以更具吸引力:它代表科学,技术,工程和数学[12]。国家科学基金会的STEM研发活动创造了新的标准,强调了四个STEM学科之间的联系[13]。随后,国家科学教育标准在美国进行了审查程序。
数学家的大脑D.Roruelle 2月4日至5日,2020年...
这本书承诺很多,只提供了很少的东西(它的承诺)。这并不是说这不是一本好阅读,它很有趣1,而只是没有提供您的期望。至少它为您提供了有关数学家大脑的任何信息,如果您考虑一下,这是一种解脱。人们建议,获得科学了解数的唯一方法是研究人脑,这据说是创造了它们的。弗雷格会在他的坟墓里转身。现在的出发点是,数学是通过对公理系统的逻辑扣除来进行的研究,即询问公理是否是真的是毫无意义的,数学家的关注是什么只是可以从中得出的内容(以及该死的后果)。可以将这种数学的观点与像素对图片像素的呈现进行比较。无疑是一个客观的演示,其不可否认的用途,例如在数字媒体中复制和操纵,但没有任何图片的线索?看到一张照片时,人的思想从某种神秘的意义上浮出水面就可以理解它。但是,当面对像素编码涉及数百万个字节的像素时,被遗忘了。它的含义都保持在黑暗中。实际上“看到”是一个古典的隐喻,它可以通过逻辑推理的长链来表现出“理解”,但对它们的含义感到困惑。在这种情况下,您经常谈论“本地理解”。该项目像GDEL所展示的那个项目一样,从而使Death-Sknell成为数学的想法,只是正式的游戏。您可以看到夹具尾部难题的不同部分相互融合,但图片本身对您来说是不透明的。将数学减少到逻辑的想法,从而使弗雷格,罗素和怀特海等人热情地追求了它的基础,甚至希尔伯特也部分地陷入了其咒语,因为他被视为对数学的形式主义观点负责。但希尔伯特从来都不是一位内心的形式主义者,他的目的是指出数学的牢固性,这意味着没有矛盾及其力量(WirMéussenWissen,Wir Wilden Wissen)。与局外人可能相信的相反,Godel的定理对生活数学没有真正的影响,只能杀死“ Matematica Principia Matematica”所建议的概念。现在要了解公理方法,可以通过在公理和假设之间进行区分来做得很好。在欧几里得的论文中,其重要性不能被超越,公理是指思想原则,假定物理空间的事实。那些公理和假设不是任意的,而是基于直觉。大
Zhiyong Zheng Kun Tian Fengxia Liu
本系列从所有领域的角度解决了与财务和应用研究有关的数学理论的新兴进步。这是一系列专着,并贡献了有关财务数学的深入探索,例如应用数学,统计,优化和科学计算,以及诸如人工智能,封闭链,云计算和大数据等技术的应用。本系列的全面理解和实用应用程序的全面应用和Finematics和Finftech的实用性为特征。本书系列涉及实用计划和公司中财务数学和Finefech的尖端应用。金融数学和金融科技书籍系列促进了新兴理论和技术数学的交流以及学术界与金融实践者之间的财务数学和网络技术的交流。它的目的是及时转移数学和计算机科学领域的最新技术,以实现财务的应用。作为一个收藏,本书系列为学术界,财务社区,与财务相关的政府员工以及其他任何希望扩大财务数学知识和资深技术知识的人提供了宝贵的资源。
CIS 5190 TA BIOS 应用机器学习 深Q学习,Alphago和Alphazero Dinesh Jayaraman -Penn Engineering
描述:我是计算机和信息科学(CIS)的二年级硕士。这将是我第二次参加此课程。我有基于NLP的项目的实习经验,并从理论和数学的角度享受解决机器学习问题。对机器学习的基本方面的这种兴趣使我对我来说既有趣又有趣。我期待一个很棒的学期!随时通过hyadav@seas.upenn.edu
12 个人工智能技术术语对于这个时代的商业人士
当我们谈论人工智能和机器学习算法时,我们谈论的是过程和我们小学学数学的时候一样。但情况更复杂。例如,谷歌使用了一种算法(基于规则的过程)为了决定哪些网站显示在搜索结果页面的顶部,机器学习技术使用不同类型的算法来得出结果。最佳结果常用算法的例子包括决策树、分类算法、回归算法等。
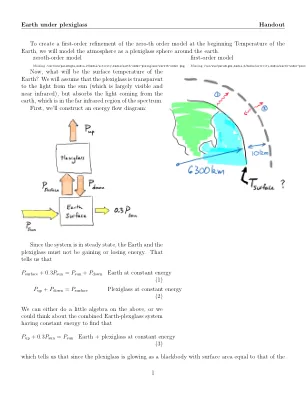
在有机玻璃讲义下的地球以创建一阶...
请注意,我们的有机玻璃温度的数学实际上与地球温度下的零级模型相同。,但现在我们正在解释现在数学的不同,因为这是地球表面的有机玻璃的温度。现在我们可以考虑有机玻璃的方程式。在这里,我们可以认识到p up = p向下,因为假设侧面在相同的温度下,各侧的有机玻璃会发出相同的速度。
一种新的逻辑、一种新的信息度量和一种基于信息的新方法来解释量子力学
摘要:新的分区逻辑与通常的布尔子集逻辑(通常仅在命题逻辑的特殊情况下出现)是双重的,因为分区和子集是范畴论的对偶。逻辑熵的新信息度量是分区的规范化定量版本。解释量子力学 (QM) 的新方法表明 QM 的数学(而不是物理)是分区数学的线性化希尔伯特空间版本。或者,反过来说,分区数学是 QM 数学的骨架版本。从逻辑到逻辑信息再到量子理论的整个过程中,关键概念是区别与无区别、确定性与不确定性或可区分性与不可区分性。分区的区别是来自底层集合的有序元素对,它们位于分区的不同块中,逻辑熵最初定义为区别的规范化数量。确定性和可区分性的同源概念贯穿于整个量子力学的数学,例如,在关键的非经典叠加概念(=本体不确定性)中,以及在费曼规则中,用于添加振幅(不可区分的选择)与添加概率(可区分的选择)。
电视和视频节目对数学学习的影响
摘要本文的主要目的是双重的:(1)介绍视频动画文献的评论并研究其在数学教育中的作用; (2)对新视频动画数学程序进行初步研究。这项研究主要是由于对美国学校中数学的恐惧猖ramp,以及通过将技术整合到数学教学中来减少这种恐惧的必要性。该研究解决了以下问题:(1)电视和视频是否有助于提高小学生理解和增加学习数学的兴趣的能力?(2)有没有办法将数学和电视相结合以使数学更有趣?和(3)学生从这种组合方法中学到多少数学?结果表明,电视和视频教育计划可以通过视觉和听觉系统提供教学信息,年轻观众可以从中学习。还表明,学生的数学学习风格与左脑/右脑理论紧密相关,左脑/右脑理论已成为教学数学和理解学生数学学习发展的关键问题。