XiaoMi-AI文件搜索系统
World File Search System量子场论中不受速子影响的非局部超微分动量算子:中性介子的情况
一个常数。这导致了量子海森堡代数的推广,其表现为位置和动量之间的扩展对易关系,即 [ x i , p j ] = i ¯ h (δ i j + βδ i j p 2 + 2 β i j p i p j ),其中 [ x i , x j ] = [ p i , p j ] = 0 [ 6 , 7 ]。这些结果还表明扩展或修改了量子力学的量子非局域性方面。事实上,有人认为,量子非局域性是 HUP 的结果,它代表了量子力学最奇怪的特性之一 [ 8 , 9 ]。这在 [ 10 ] 中已得到详细讨论,并被发现与 Franson 实验 [ 11 ] 中出现的重合率版本一致。已经检测到 GUP 对角动量代数和两个部分系统(量子比特和量子三元组)的贝尔算子的平方及其期望值的影响。违反贝尔不等式可能是制定量子引力的重要工具,而且,Stern-Gerlach 实验的精度限制了 GUP 参数 β 的值。应该强调的是,量子非局域性已经
算子代数量子误差校正的稳定器形式
我们引入了一种稳定器形式,用于称为算子代数量子纠错 (OAQEC) 的通用量子纠错框架,它概括了 Gottesman 对传统量子纠错码 (QEC) 的公式和 Poulin 对算子量子纠错和子系统代码 (OQEC) 的公式。该构造生成混合经典量子稳定器代码,我们制定了一个定理,该定理完全描述了给定代码可纠正的 Pauli 错误,概括了 QEC 和 OQEC 稳定器形式的基本定理。我们发现了受形式主义启发的 Bacon-Shor 子系统代码的混合版本,并应用该定理得出了给出此类代码距离的结果。我们展示了一些最近的混合子空间代码构造如何被形式主义捕获,我们还指出了它如何扩展到量子比特。
FERMI品种的代数特性,用于周期性图算子
最近,其中一位作者引入了一种新的方法来研究多项式的不可约性,为ℓ2z d上的形式-Δ + V的周期性操作员获得了几个新结果。在这种情况下,刘证明,对于d = 2,费米品种在每个能级λ不可还原,除了平均能量水平。他还证明,当d≥3时,费米品种对于每个级别的λ不可还原[22]。特别是对于此类操作员,因此,Bloch品种在任意维度[22]中是不可还原的。[22]中的结果提供了关于离散设置中费米和Bloch品种不可约性的猜想的完整证明,如许多文章[3,4,10,13,16,18]中所述。
量子和经典的波动算子表示...
在描述物理系统时,数学表示的选择非常重要,而这种选择通常由手头问题的性质决定。在这里,我们研究了鲜为人知的量子动力学波算子表示,并探索了它与量子动力学标准方法(如维格纳相空间函数)的联系。该方法以密度矩阵的平方根为中心,因此比标准表示具有几个不寻常的优势。通过将其与从量子信息中引入的净化技术相结合,我们能够获得许多结果。这种形式不仅能够在量子和经典动力学的相和希尔伯特空间表示之间提供自然的桥梁,我们还发现波算子表示可以导致实时间和虚时间动力学的新型半经典近似,以及与经典极限的透明对应。然后证明存在许多场景(例如热化),其中波算子表示具有等效的幺正演化,这对应于密度矩阵的非线性实时动力学。我们认为,波算子提供了一种将以前不相关的表示联系起来的新视角,并且是无法以其他方式保证正性的场景(例如混合)的自然候选模型。
开放量子系统中的算子增长 - CDN
引言:传统上,量子多体系统的研究集中于预测少体可观测量,如局部相关函数。最近,受量子热化和混沌[1]、量子系统的经典模拟[2]和量子引力[3]中基本问题的启发,物理学家们转向了一项互补的研究:量化多体动力学本身的复杂性。这一研究的核心是量子信息扰乱的概念;在几乎所有相互作用的多体量子系统中,最初在局部算子中编码的信息会逐渐变得高度非局部[4-6]。值得注意的是,最近的实验进展使得直接测量扰乱成为可能——这项任务最常见的是利用时间倒退演化[7-14],但也可以使用系统的多个副本[15-17]或随机测量[18,19]来执行。在这样的系统中,扰乱动力学、外部退相干和实验噪声之间的相互作用引发了一个基本问题:开放量子系统中量子信息扰乱的本质是什么[13,16,20 – 31]?在本文中,我们引入了一个基于算子尺寸分布的通用框架[32 – 35],用于捕捉局部误差对扰乱动力学的影响。具体来说,我们推测混沌多体系统中误差的传播从根本上受时间演化算子的尺寸分布控制,与微观误差机制无关。我们的框架立即为 Loschmidt 回声[36 – 38] 和非时序相关 (OTOC) 函数 [39,40] 提供了预测。具体来说,我们预测 Loschmidt 回声的衰减(用于测量与时间向后演化相关的保真度)发生在
使用扩展维纳和拉普拉斯算子进行脑肿瘤分割
Zhao 等 [45] 2013 年基准 BRATS 数据 Patch-wise 卷积神经网络 总体 (0.81) 准确率 Manic 等 [46] 阐述了基于萤火虫的灰度图像分割方法
用于参数化量子算子发现的混合多目标遗传规划
量子信息的处理由量子电路定义。对于当前量子设备上的应用,这些通常是参数化的,即它们包含具有可变参数的操作。设计这样的量子电路和聚合的高级量子算子是一项具有挑战性的任务,需要大量的量子信息理论知识,前提是可以通过分析找到多项式大小的解。此外,找到一个具有低计算成本的精确解决方案代表着一个重大的权衡,特别是对于当前一代量子计算机而言。为了应对这些挑战,我们提出了一种多目标遗传编程方法(与数值参数优化器混合)来自动合成参数化量子算子。为了证明所提出方法的优势,将其应用于混合量子经典算法的量子电路,然后与分析解决方案和非混合版本进行比较。结果表明,与非混合版本相比,我们的方法产生了更多样化的解决方案和更准确的量子算子,甚至达到了分析基线的质量。
库普曼算子理论的车辆应用
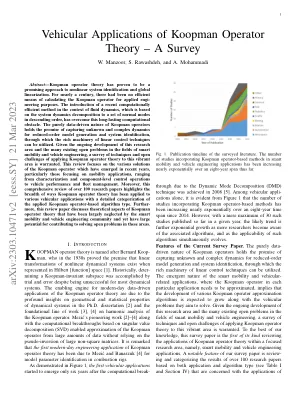
摘要 — 库普曼算子理论已被证明是一种很有前途的非线性系统辨识和全局线性化方法。近一个世纪以来,一直没有有效的方法来计算用于应用工程目的的库普曼算子。最近在流体动力学背景下引入了一种计算效率高的方法,该方法基于将系统动力学分解为一组按降序排列的正态模式,克服了这一长期存在的计算障碍。库普曼算子纯数据驱动的性质有望捕捉未知和复杂的动力学以进行降阶模型生成和系统辨识,从而利用线性控制技术的丰富机制。鉴于该研究领域的不断发展以及智能移动和车辆工程领域存在的许多未解决的问题,有必要对将库普曼算子理论应用于这一充满活力的领域的技术和开放挑战进行调查。本综述重点介绍了近年来出现的 Koopman 算子的各种解决方案,特别是那些专注于移动应用的解决方案,从特性和组件级控制操作到车辆性能和车队管理。此外,这篇对 100 多篇研究论文的全面回顾突出了 Koopman 算子理论在各种车辆应用中的应用范围,并对所应用的基于 Koopman 算子的算法类型进行了详细分类。此外,这篇评论论文讨论了 Koopman 算子理论的理论方面,这些理论方面在很大程度上被智能移动和车辆工程界忽视,但在解决这些领域的未解决问题方面具有巨大的潜力。
格子量子场论经典模拟中插值算子的量子优化构造策略
最近有人提出,嘈杂的中型量子计算机可用于优化经典计算机上格子量子场论 (LQFT) 计算的插值算子构造。这里,开发并实施了该方法的两种具体实现。第一种方法是最大化插值算子作用于真空状态与目标本征态所创建状态的重叠或保真度。第二种方法是最小化插值状态的能量期望值。这些方法在 (1 + 1) 维中针对单一味大质量 Schwinger 模型的概念验证计算中实现,以获得理论中矢量介子状态的量子优化插值算子构造。虽然在没有量子门误差噪声的情况下,保真度最大化是更好的选择,但在概念验证计算中,能量最小化对这些影响更具鲁棒性。这项工作具体展示了中期量子计算机如何用于加速经典 LQFT 计算。
量子状态制备和对角算子的非自动进化
实现基于统一的量子量子设备上的非单身转换对于模拟各种物理问题至关重要,包括开放量子系统和亚范围量子量子状态。我们提出了一种基于扩张的算法,用于使用仅使用一个Ancilla量子的概率量子计算模拟非自动操作。我们利用奇异值分解(SVD)将任何通用量子运算符分解为两个单一操作员和对角线非单身操作员的产物,我们证明可以通过对角度扩张的空间中的对角线统一操作员来实施,这可以实现。扩张技术增加了计算中的Qubit数量,因此,我们的算法将扩张空间中所需的操作限制为对角统一操作员,该操作员已知电路分解。我们使用此算法在具有高忠诚度的量子设备上准备随机的亚标准化两级状态。此外,我们介绍了在dephasing通道中的两级开放量子系统的准确非单身动力学和在量子设备上计算的振幅阻尼通道的准确非单身动力学。提出的算法对于可以轻松计算SVD时实施一般的非独立操作是最有用的,在嘈杂的中间规模量子计算时代,大多数运营商就是这种情况。