机构名称:
¥ 1.0
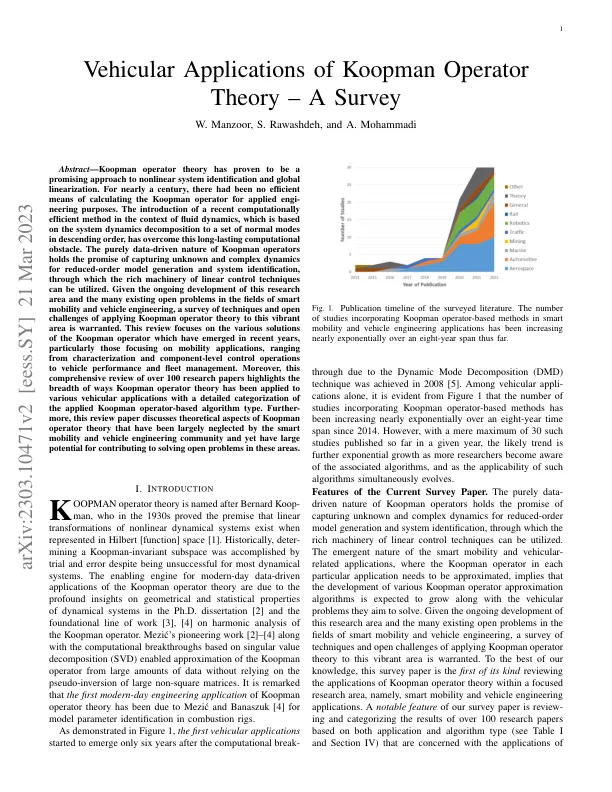
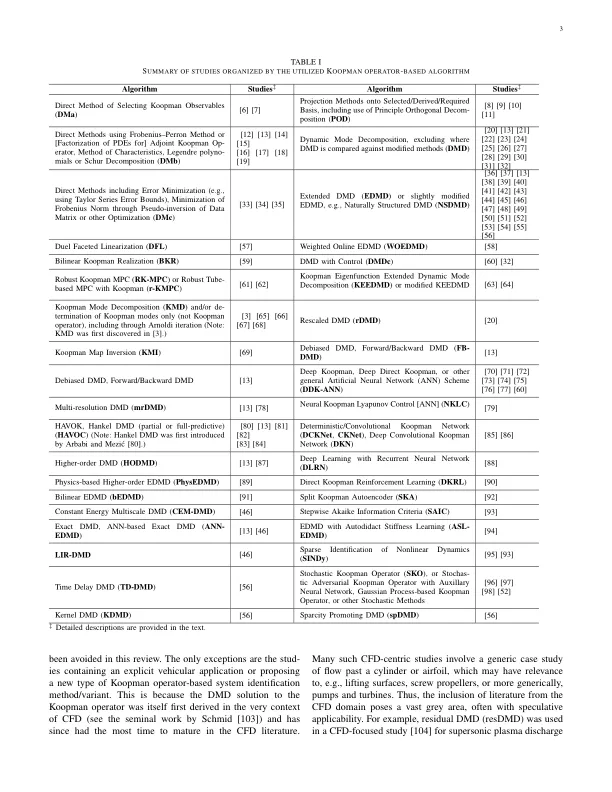
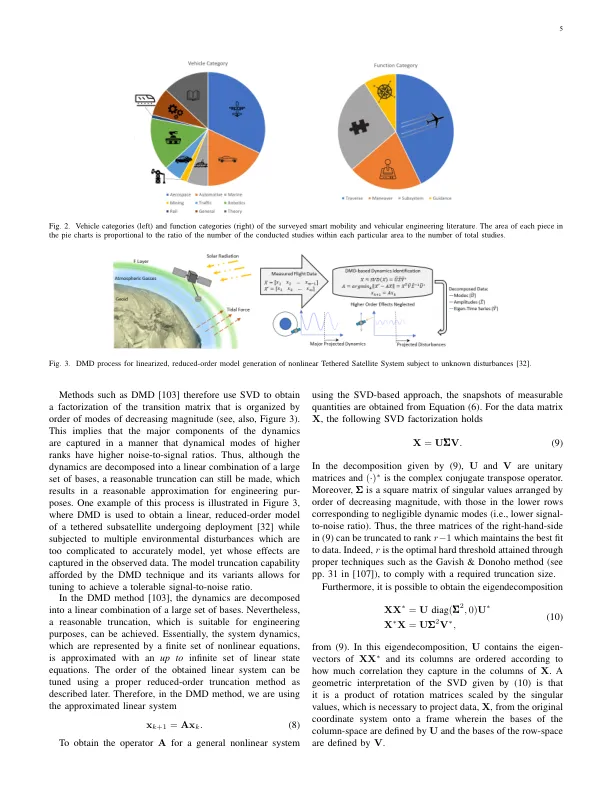
摘要 — 库普曼算子理论已被证明是一种很有前途的非线性系统辨识和全局线性化方法。近一个世纪以来,一直没有有效的方法来计算用于应用工程目的的库普曼算子。最近在流体动力学背景下引入了一种计算效率高的方法,该方法基于将系统动力学分解为一组按降序排列的正态模式,克服了这一长期存在的计算障碍。库普曼算子纯数据驱动的性质有望捕捉未知和复杂的动力学以进行降阶模型生成和系统辨识,从而利用线性控制技术的丰富机制。鉴于该研究领域的不断发展以及智能移动和车辆工程领域存在的许多未解决的问题,有必要对将库普曼算子理论应用于这一充满活力的领域的技术和开放挑战进行调查。本综述重点介绍了近年来出现的 Koopman 算子的各种解决方案,特别是那些专注于移动应用的解决方案,从特性和组件级控制操作到车辆性能和车队管理。此外,这篇对 100 多篇研究论文的全面回顾突出了 Koopman 算子理论在各种车辆应用中的应用范围,并对所应用的基于 Koopman 算子的算法类型进行了详细分类。此外,这篇评论论文讨论了 Koopman 算子理论的理论方面,这些理论方面在很大程度上被智能移动和车辆工程界忽视,但在解决这些领域的未解决问题方面具有巨大的潜力。
库普曼算子理论的车辆应用
主要关键词