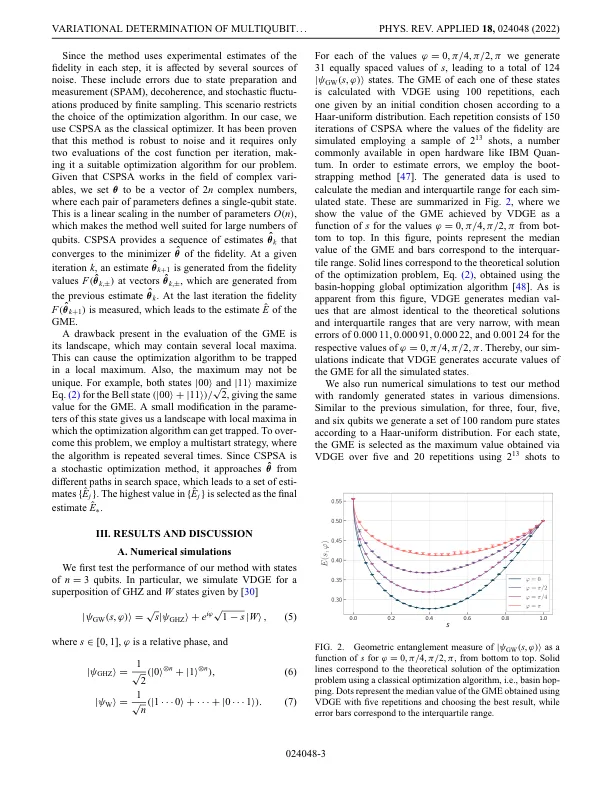
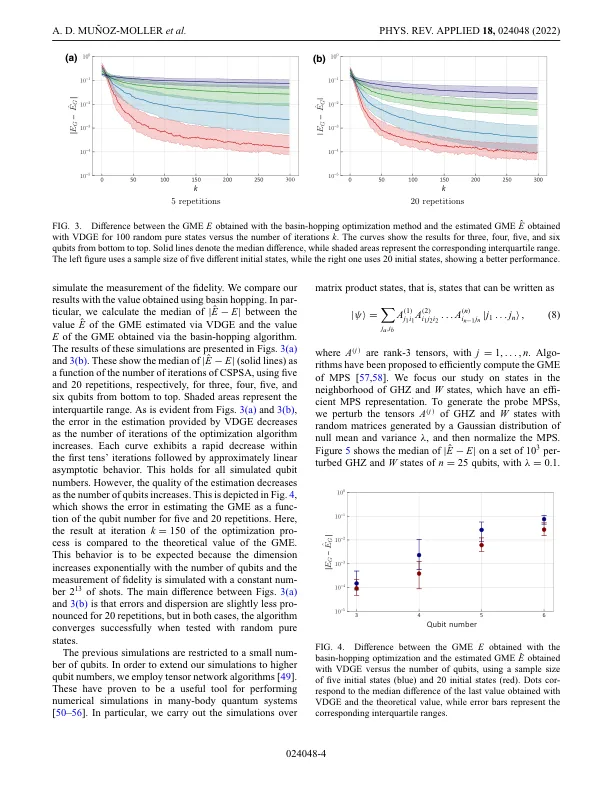
机构名称：
¥ 1.0
纠缠的量子状态[1]被认为是反对量子力学的完整性的论点[2]，如今被认为是该理论的区分特征。纠缠也被广泛认为是量子计算和量子信息研究中的核心资源之一[3]；量子算法（例如Shor算法[4]）的成功与量子计算机中的非局部门的适当实现相关，而量子电视[5]和量子密钥分布等方案[6]依赖于两个或更多各方之间的纠缠状态。纠缠。由于纠缠在量子力学及其许多可行应用中所起的作用，已经开发了几种方法来量化和识别它。基于部分转置映射的负态性的Peres-Horodecki定理[10，11]允许在Qubit-Qubit和Qubit-Qutrit纯或混合量子状态中存在纠缠，但对于较高尺寸的biTemential biatsiate biatsional biatsiate butemential butions of证明。与此一起，部分转置映射对应于非物理操作，因此不能直接实施实验。也可以采用铃铛不平等[12]来检测已知状态的纠缠，这需要解决优化问题。在这里，违规信号
噪声中间量子计算机中多等级几何纠缠的变分确定
主要关键词
相关文件推荐
