机构名称：
¥ 1.0
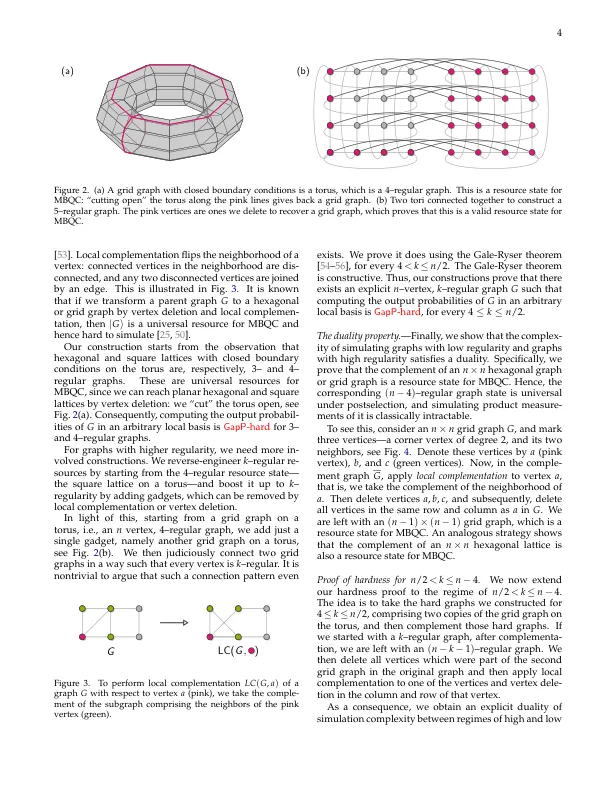
纠缠是量子系统的物理特性之一，它决定了模拟量子系统的计算难度。但是，虽然特定算法（尤其是张量网络算法）的运行时间明确取决于系统中的纠缠量，但尚不清楚这种联系是否更深，而且纠缠还会导致固有的、与算法无关的复杂性。在这项工作中，我们定量地将某些量子系统中存在的纠缠与模拟这些系统的计算复杂性联系起来。此外，我们完全将纠缠和复杂性表征为系统参数的函数。具体来说，我们考虑模拟 n 个量子比特上 k 个正则图状态的单量子比特测量的任务。我们表明，随着规律性参数从 1 增加到 n − 1，在 k = 3 时，会出现从低纠缠度的简单状态到高纠缠度的困难状态的急剧转变，而在 k = n − 3 时，又会转变回简单和低纠缠度。作为一项关键的技术成果，我们证明了低规律性和高规律性之间规则图状态模拟复杂度的对偶性。
纠缠产生的复杂相变
主要关键词
相关文件推荐
