机构名称：
¥ 1.0
大量研究了各类特殊函数（如勒让德多项式）的性质。此外，这个无穷级数似乎不能用简单函数表示，只能用数值计算。总之，在这项工作中，我们研究了由表面电荷密度均匀的“北”半球面产生的静电势的性质。这个问题引起了广大静电学或电动力学领域研究人员和教育工作者的兴趣 20 。我们利用一种数学方法，充分利用了物体的轴对称性，推导出适用于某些特殊情况的静电势的精确紧致解析表达式。我们还推测了空间中任意一点的通解的性质，暗示它可以计算为无穷级数，但不是紧致的解析形式。作为该方法的简单副产品，我们以公式 (12) 中的表达式形式获得了一个有趣的数学积分公式。
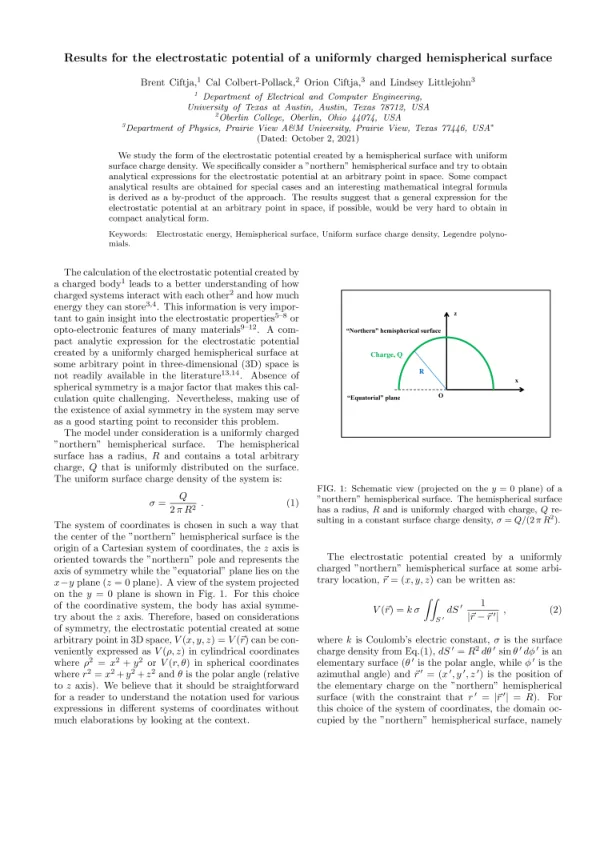
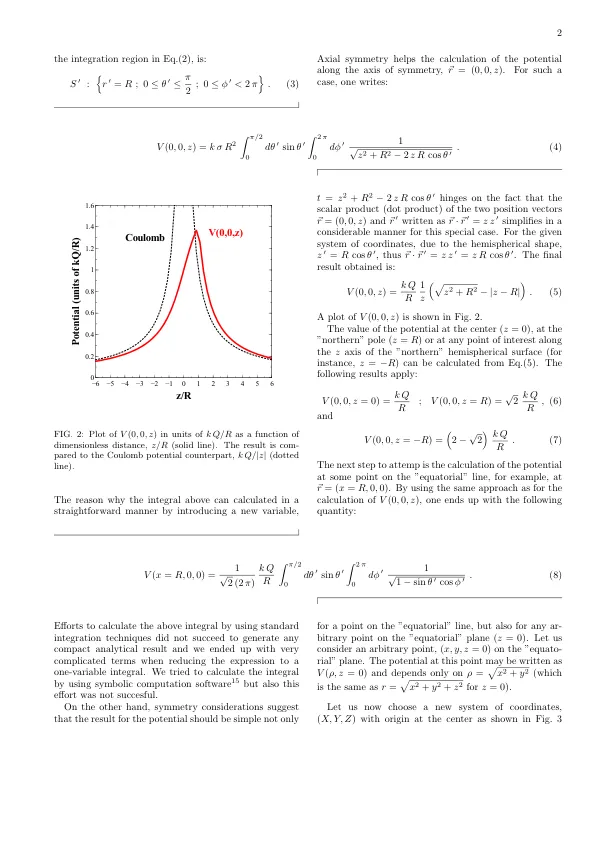
公式（2）中的积分区域为
主要关键词
相关文件推荐
