机构名称：
¥ 1.0
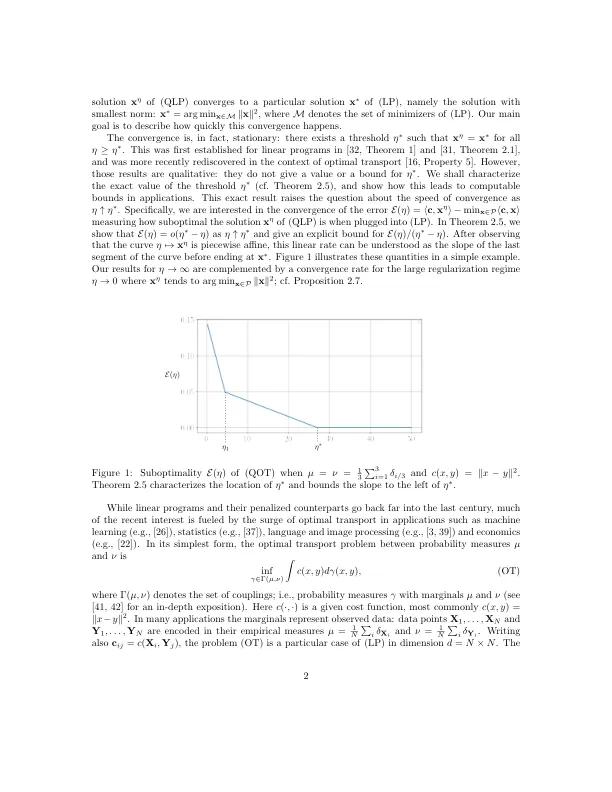
具有二次正则化的线性程序由于其在最佳运输方面的应用而引起了新的兴趣：与熵正则化不同，平方惩罚导致最佳运输耦合的近似值稀少。众所周知，当正则化参数趋于零时，在任何多层层上的四个正规化线性程序的解会收敛到线性程序的最小值解决方案。但是，该结果仅是定性的。我们的主要结果通过指定正规化参数的确切阈值来量化收敛性，然后正则化解决方案还求解线性程序。此外，我们在阈值之前绑定了调节解的次优性。这些结果与大规模正规化制度的收敛速率相辅相成。我们将一般结果应用于最佳传输的设置，在那里我们阐明了阈值和次级次要性如何取决于数据点的数量。
二次正规化线性程序的定量收敛
主要关键词
相关文件推荐
