XiaoMi-AI文件搜索系统
World File Search System伽马射线对运算放大器 741 和定时器 555 IC 的影响
Esra KENDİR TEKGÜL * Şerafettin YALTKAYA ** 收到日期:2022 年 3 月 31 日;修订日期:2022 年 12 月 26 日;接受日期:2023 年 3 月 30 日 摘要:在 Co-60 源的伽马射线辐射下研究了商用 555 单定时器和 741 运算放大器 (op-amp)。使用的最大总剂量为 2 kGy 和 4 kGy 进行辐照。观察到 555 单定时器电路频率的异常行为,在 744 Gy 伽马射线辐射下从 202 Hz 降至 195 Hz。在 741 运算放大器电路的结果中,741 运算放大器的幅度信号在 4 kGy 伽马剂量下显示最大值 -0.054 dB,其斜率从 4 V/µs 降至 0.65 V/µs。555 单定时器具有两个 pn 结,这导致 555 单定时器很容易受到伽马辐射的影响。因此,必须对集成电路进行测试以确定其在辐射环境中的电阻极限。
Qompress:利用部分和混合基数运算减少通信量的 Ququarts 高效编译
量子计算正处于资源有限的时代。当前的硬件缺乏高保真门、长相干时间以及执行有意义计算所需的计算单元数量。现代量子设备通常使用二进制系统,其中每个量子位都存在于 | 0 ⟩ 和 | 1 ⟩ 状态的叠加中。然而,通过以不同的方式操纵系统,通常可以访问同一物理单元中的 | 2 ⟩ 甚至 | 3 ⟩ 状态。在这项工作中,我们考虑通过压缩方案自动将两个量子位编码为一个四状态量子。我们使用量子最优控制来设计高效的概念验证门,完全复制这些编码量子位上的标准量子位计算。我们扩展了量子比特编译方案,以便在由量子比特和量子门组成的任意混合基数系统上高效路由量子比特,从而减少通信并最大限度地减少由较长持续时间的量子门引入的额外电路执行时间。结合这些编译策略,我们引入了几种方法来寻找有益的压缩,将计算和通信导致的电路错误减少高达 50%。这些方法可以将有限的近期机器上可用的计算空间增加高达 2 倍,同时保持电路保真度。
适用于低压应用的高增益两级体驱动运算跨导放大器 (OTA) 的设计
本论文由雪城大学 SURFACE 免费提供给您,供您开放访问。雪城大学 SURFACE 的授权管理员已接受本论文并将其收录到论文 - ALL 中。如需更多信息,请联系 surface@syr.edu。
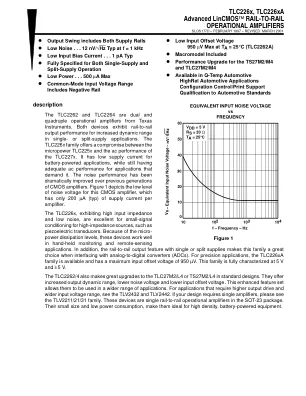
高级 LinCMOS 轨至轨运算放大器数据表 (Rev. D)
电源电压,V DD+ (见注释 1)8 V 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。电源电压,V DD– (见注 1)–8V。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。差分输入电压,V ID (见注释 2)± 16 V 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。输入电压,V I (任何输入,见注释 1)V DD– – 0.3 V 至 V DD+ 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。...... div>...输入电流,I I (每个输入) ± 5 mA .. < /div>............。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.输出电流,I O ± 50 mA ..........< div> 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.流入 V DD+ 的总电流 ± 50 mA .... div>........。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。V DD– ± 50 mA 输出的总电流。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。25°C(或以下)时的短路电流持续时间(见注3)无限制。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。连续总耗散 请参阅耗散额定值表。。。。。。。。。。。。。。。。。。。。。。。。。。。。...................工作自然空气温度范围,TA:C后缀0°C至70°C。......。。。。。。。。。。。。。。。。。。。。。。。。........我后缀 –40 ° C 至 125 ° C .................................Q 后缀 –40 ° C 至 125 ° C .。。。。。。。。。。。。。。。。。。。。。。。。...........M 后缀 –55 ° C 至 125 ° C ............。。。。。。。。。。。。。。。。。。。。。。存储温度范围,T stg –65 ° C 至 150 ° C 。............。。。。。。。。。。。。。。。。。。。。。。。。。...... div>......引线温度 1,6毫米(1/16 英寸)距离外壳 10 秒:D、N、P 和 PW 封装 260 ° C 。......J、JG、U 和 W 封装 300 ° C 。。。。。。。
AB 类运算放大器:低 Iq 音频解决方案
以下是 Quan 电路的摘要:该电路通过感测电压使输出晶体管放大器的静态集电极电流保持恒定,该电压是在与输出晶体管集电极串联的电阻上产生的。采用差分放大器产生代表该电压的第一信号,该信号由通过对放大器输出电压敏感的零电压交叉检测器控制的电路采样和保持。采样和保持的信号相对于可调参考电压反转和积分,产生第二信号。该第二信号控制通过分压器网络中连接的晶体管的电流,为输出晶体管提供基极偏置电压。
A-unital 运算和量子条件熵
负量子条件熵状态是信息论任务(如超密集编码、状态合并和单向纠缠蒸馏)的关键要素。在这项工作中,我们提出一个问题:如何检测一个通道是否可用于准备负条件熵状态?我们通过引入 A-unital 通道类来回答这个问题,我们表明它们是条件熵非递减通道中最大的一类。我们还证明了 A-unital 通道正是具有非负条件熵的状态类的完全自由操作。此外,我们研究了 A-unital 通道与资源纠缠理论相关的其他通道类之间的关系。然后,我们证明了 ACVENN 的类似结果:这是一类先前定义的相关状态,并将状态的最大和最小条件熵与其冯诺依曼熵联系起来。A-unital 通道的定义自然有助于确定此类通道的成员资格。因此,我们的工作对于在条件熵的背景下检测资源丰富的通道具有价值。
使用物理系统的能量状态编码双量子比特逻辑状态和量子运算
摘要:本文介绍了一种新颖的编码方案,该方案允许单个量子系统对多量子比特寄存器进行编码。这可以更有效地利用资源,并在设计量子系统时节省成本。该方案基于使用通过在半导体材料中引入杂质形成的离散能谱的电荷自由度来编码逻辑量子态的概念。我们提出了一种执行单量子比特操作和受控双量子比特操作的机制,提供了一种使用由 Rabi 振荡产生的适当脉冲来实现这些操作的机制。使用 IBM 的 Armonk 单量子比特量子计算机模拟上述架构,将两个逻辑量子态编码为 Armonk 量子比特的能量态,并使用自定义脉冲执行一量子比特和两量子比特量子操作。
低压低功耗高增益运算放大器的设计...
摘要 本文介绍了一种高增益运算跨导放大器结构。为了实现具有改进的频率响应的低压操作,在输入端使用体驱动准浮栅 MOSFET。此外,为了实现高增益,在输出端使用改进的自共源共栅结构。与传统的自共源共栅相比,所用的改进的自共源共栅结构提供了更高的跨导,这有助于显著提高放大器的增益。改进是通过使用准浮栅晶体管实现的,这有助于缩放阈值,从而增加线性模式晶体管的漏极-源极电压,从而使其变为饱和状态。这种模式变化提高了自共源共栅 MOSFET 的有效跨导。与传统放大器相比,所提出的运算跨导放大器的直流增益提高了 30dB,单位增益带宽也增加了 6 倍。用于放大器设计的 MOS 模型采用 0.18µm CMOS 技术,电源为 0.5V。
公告网络计量生成器运算符
公告日期发布日期:2021年10月25日至:所有许可的电力分销商所有其他有关方面re:有资格在分销客户运行的地方进行净计量,但不拥有该公告的可再生能源生成设施。该公告规定了安大略省能源委员会(OEB)员工的观点,可以使自己的能量客户提供“有资格的客户”,但要运行“有资格的机器人”。发电设施。1。背景在安大略省,净计量由O. Reg管辖。541/05(净计量)根据1998年的《安大略省能源委员会法》(OEB法案)进行。 这是一种计费安排,分销商的客户(在规定中称为“合格发电机”)可以为客户在客户将客户传达到分销商的分配系统中产生的任何超额可再生电力的价值而获得电力信用。 OEB员工通过创新沙箱收到了请求,以指导电力分销商是否可以视为“合格的发电机”,因此如果客户运行但不拥有发电设施,则能够参与净计量。 2。 合格的发电机不必拥有OEB法案将“生成器”定义为“拥有或经营生成设施的人”的发电设施(重点添加)。 使用“或”表示一个人不需要拥有并操作生成设施才能被视为“发电机”;一个就足够了。541/05(净计量)根据1998年的《安大略省能源委员会法》(OEB法案)进行。这是一种计费安排,分销商的客户(在规定中称为“合格发电机”)可以为客户在客户将客户传达到分销商的分配系统中产生的任何超额可再生电力的价值而获得电力信用。OEB员工通过创新沙箱收到了请求,以指导电力分销商是否可以视为“合格的发电机”,因此如果客户运行但不拥有发电设施,则能够参与净计量。2。合格的发电机不必拥有OEB法案将“生成器”定义为“拥有或经营生成设施的人”的发电设施(重点添加)。使用“或”表示一个人不需要拥有并操作生成设施才能被视为“发电机”;一个就足够了。的确,在一个发电设施的所有权和运营依赖于不同的人的情况下,OEB签发单独的发电许可的做法。在这种情况下,操作员将是根据其与第三方所有者的法律安排条款确定
b'摘要。本文提出了将对称密码代数方程转化为QUBO问题的方法。将给定方程f 1 ,f 2 ,... ,fn转化为整数方程f \xe2\x80\xb2 1 ,f \xe2\x80\xb2 2 ,... ,f \xe2\x80\xb2 n后,对每个方程进行线性化,得到f \xe2\x80\xb2 lin i = lin ( f \xe2\x80\xb2 i ),其中lin表示线性化运算。最后,可以得到 QUBO 形式的问题,即 f \xe2\x80\xb2 lin 1 2 + \xc2\xb7 \xc2\xb7 \xc2\xb7 + f \xe2\x80\xb2 lin n 2 + Pen ,其中 Pen 表示在方程线性化过程中获得的惩罚,n 是方程的数量。在本文中,我们展示了一些分组密码转换为 QUBO 问题的示例。此外,我们展示了将完整的 AES-128 密码转换为 QUBO 问题的结果,其中等效 QUBO 问题的变量数量等于 237,915,这意味着,至少在理论上,该问题可以使用 D-Wave Advantage 量子退火计算机解决。不幸的是,很难估计这个过程所需的时间。'
b'摘要。本文提出了将对称密码代数方程转化为QUBO问题的方法。将给定方程f 1 ,f 2 ,... ,fn转化为整数方程f \xe2\x80\xb2 1 ,f \xe2\x80\xb2 2 ,... ,f \xe2\x80\xb2 n后,对每个方程进行线性化,得到f \xe2\x80\xb2 lin i = lin ( f \xe2\x80\xb2 i ),其中lin表示线性化运算。最后,可以得到 QUBO 形式的问题,即 f \xe2\x80\xb2 lin 1 2 + \xc2\xb7 \xc2\xb7 \xc2\xb7 + f \xe2\x80\xb2 lin n 2 + Pen ,其中 Pen 表示在方程线性化过程中获得的惩罚,n 是方程的数量。在本文中,我们展示了一些分组密码转换为 QUBO 问题的示例。此外,我们展示了将完整的 AES-128 密码转换为 QUBO 问题的结果,其中等效 QUBO 问题的变量数量等于 237,915,这意味着,至少在理论上,该问题可以使用 D-Wave Advantage 量子退火计算机解决。不幸的是,很难估计这个过程所需的时间。'