机构名称:
¥ 5.0
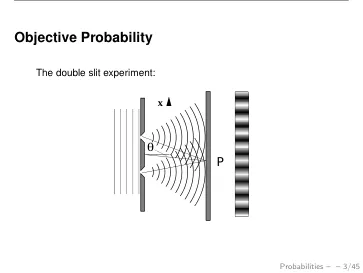
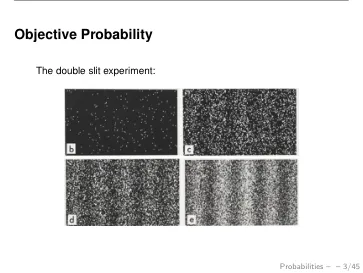
动机:人工智能系统需要推理它们知道或不知道的事情。不确定性可能有很多来源:环境可能是随机的,因此无法确定性地预测未来。环境只能部分观察,导致对其余部分的不确定性。当环境包括其他代理或人类时尤其如此,而这些代理或人类的内涵是无法直接观察到的。系统只能收集有限的数据,必然导致不确定的模型。我们需要对所有这些都进行微积分。概率是正确的微积分。实际上,平凡的贝叶斯规则原则上告诉我们如何处理信息:每当我们对某事有先前的不确定性,然后获得新信息时,贝叶斯规则就会告诉我们如何更新我们的知识。这个概念非常普遍,它包括机器学习、(贝叶斯)强化学习、贝叶斯过滤(卡尔曼和粒子过滤器)等的大部分内容。当然,需要注意的是,在实践中计算或近似这种贝叶斯信息处理。在本讲座中,我们将介绍一些概率的基础知识,其中许多您之前在其他课程中已经学过。因此,目的也是回顾和介绍符号。我们介绍的内容对于后面关于老虎机、强化学习、图形模型和关系概率模型的讲座至关重要。
人工智能概率
主要关键词