机构名称：
¥ 1.0
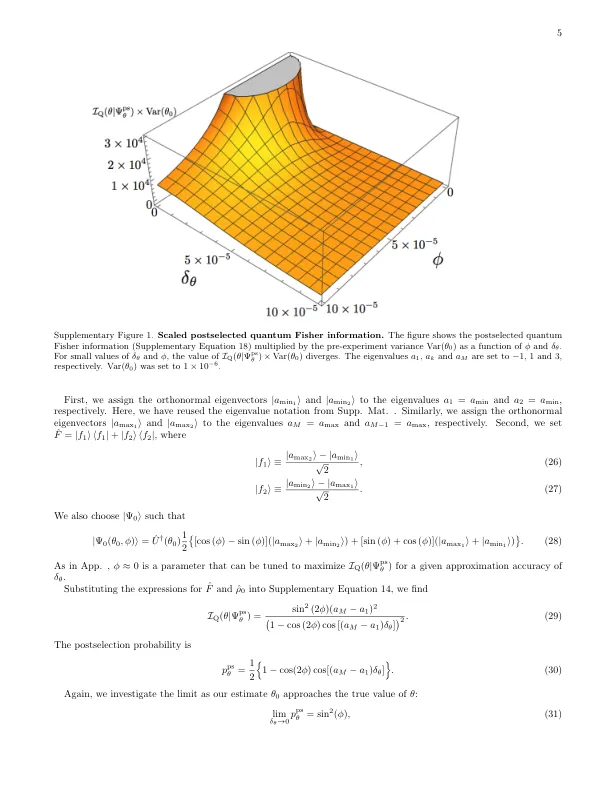
根据补充方程 24，如果在补充方程 18 中 δ θ 和 φ 先趋近于 0，则 IQ ( θ | Ψ ps θ ) 趋近于无穷大。有几点需要注意。首先，IQ ( θ | Ψ ps θ ) 在两个有序极限中发散。在任何实际实验中，都不能盲目地设置 φ = 0，而必须根据 θ 的估计值选择 φ。其次，如果 δ θ ≈ 0，则 θ 0 ≈ θ ，并且我们初始估计 θ 0 的实验前方差 Var(θ 0) 必须很小。也就是说，我们在开始实验时就掌握了有关 θ 的大量信息。在 Cram´er-Rao 界的指导下，我们预计，在一个有用的实验中，IQ ( θ | Ψ ps θ ) 会变大，而 1 / Var( θ 0 ) < IQ ( θ | Ψ ps θ )。补充图 1 显示了 IQ ( θ | Ψ ps θ ) × Var( θ 0 ) 作为 φ 和 δ θ 的函数，适用于实验，其中 a 1 = − 1、ak = 1、a M = 3 且 Var( θ 0 ) = 10 − 6 。如果 θ 0 在几个 σ θ 0 ≡ p 之内
量子在后选定计量方面的优势
主要关键词
相关文件推荐
