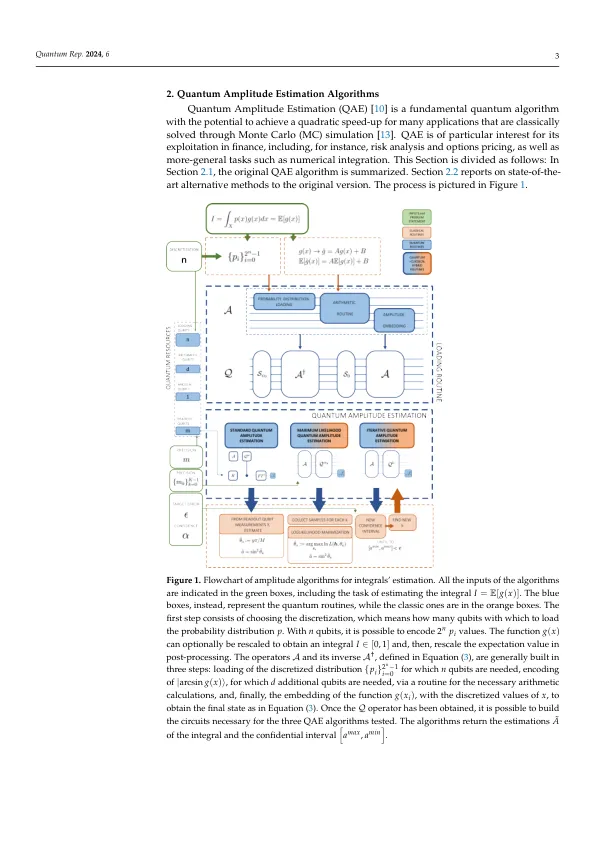
摘要：量子振幅估计（QAE）算法是一种主要的量子算法，旨在实现二次加速。直到实现易于断层的量子计算为止，与经典的蒙特卡洛（MC）具有竞争力一直难以捉摸。已经开发出替代方法，以便在保持有利的理论规模的同时需要更少的资源。我们将标准QAE算法与两个嘈杂的中间尺度量子（NISQ）在数值集成任务上的友好版本与大都会的蒙特卡洛技术 - 黑斯廷斯作为经典基准。分别根据样品数量，计算时间和解决方案所需的量子电路的长度来评估算法。在11 Quibent的捕获量子计算机上测试了两个QAE替代方案的有效性，以验证哪种解决方案可以首先在积分估计问题中加快速度。我们得出的结论是，对于使用阶段估计常规而言，另一种方法是可取的。的确，最大似然估计保证了量子电路的长度与积分估计中的精度以及对噪声的更大阻力之间的最佳权衡。