机构名称:
¥ 1.0
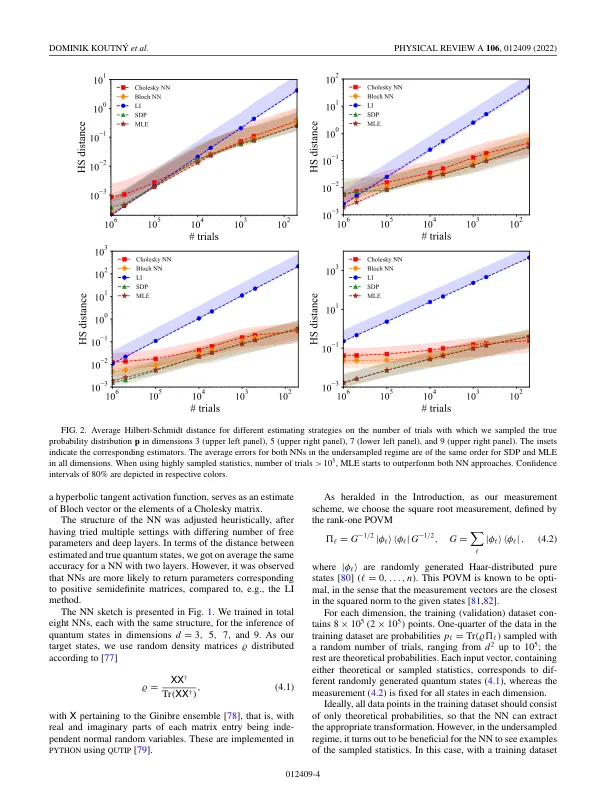
现代量子技术利用量子系统的独特特性来实现经典策略无法达到的性能。这一潜在优势取决于创建、操纵和测量量子态的能力。该领域的任何实验程序都需要对这些步骤进行可靠的认证:这正是量子态层析成像 (QST) 的领域 [1]。QST 的目标是通过对系统有限组相同副本进行测量来估计未知的量子态。如果状态由密度矩阵 ϱ 描述,位于 ad 维希尔伯特空间中,则需要 O(d/ε) 个副本才能获得 ϱ 的估计值,且误差(理解为总变分距离)小于 ε[2]。这清楚地说明了 QST 对大规模系统的资源需求。从广义上讲,QST 是一个逆问题 [3-5]。因此,线性反演 [6] 可能是该主题最直观的方法。然而,它也有一些缺点:它可能报告非物理状态,并且无法通过分析确定估计的均方误差界限。为了绕过这些缺点,可以使用各种有用的 QST 方法,例如贝叶斯断层扫描 [ 7 , 8 ]、压缩感知 [ 9 , 10 ] 或矩阵积状态 [ 11 , 12 ],尽管最大似然估计 (MLE) 仍然是最常用的方法 [ 13 , 14 ]。从现代的角度来看,QST 本质上是一个数据处理问题,试图从
神经网络量子态断层扫描
主要关键词