机构名称:
¥ 1.0
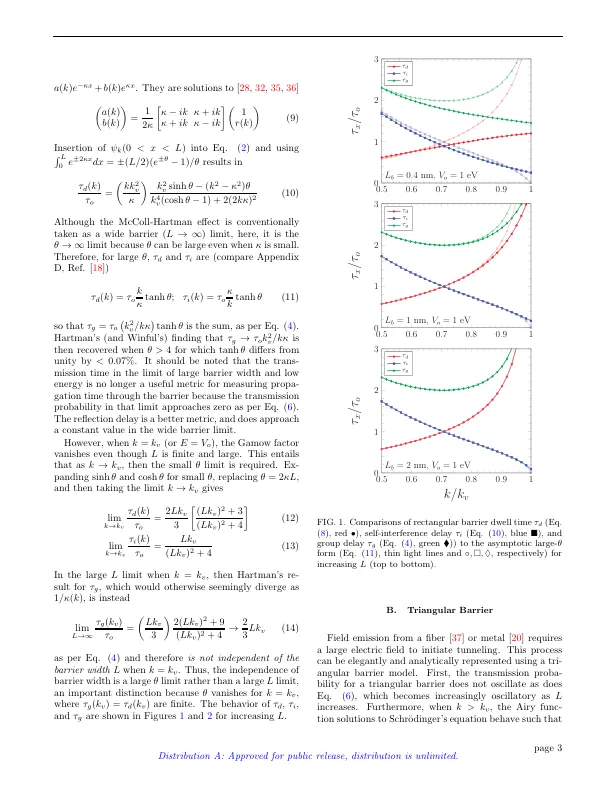
使用 Gamow 因子 θ ( k ) 重新进行了 Winful 的分析,以便进行推广。第三,对高场电子发射特性势垒重复 Gamow 分析。有几个候选势垒:(i) 镜像电荷或肖特基-诺德海姆 (SN) 势垒[20]:它描述金属 [21] 和半导体 [22] 的场发射,具有半解析的 Gamow 因子 θ ( k ),但透射 t ( k ) 和反射 r ( k ) 系数必须通过数值计算;(ii) Eckart 势垒[23]:它是非对称势垒,对于它,t(k) 和 r(k) 是解析的,但 Gamow 因子 θ ( k ) 必须通过数值计算; (iii) 三角势垒或 Fowler-Nordheim (FN) 势垒 [21] 用于场发射:它忽略了镜像电荷效应,但 t(k)、r(k) 和 θ(k) 都是完全解析的。因此,只有所选的三角势垒 (iii) 才是高场条件下场发射的简单、纯解析表示(并且是隧道波力学最具代表性的例子 [24, 25])。因此,FN 形式 [26–28] 用于开发和分析停留时间 τ d 和自干扰时间 τ i。
重新评估场发射的哈特曼效应
主要关键词