机构名称:
¥ 1.0
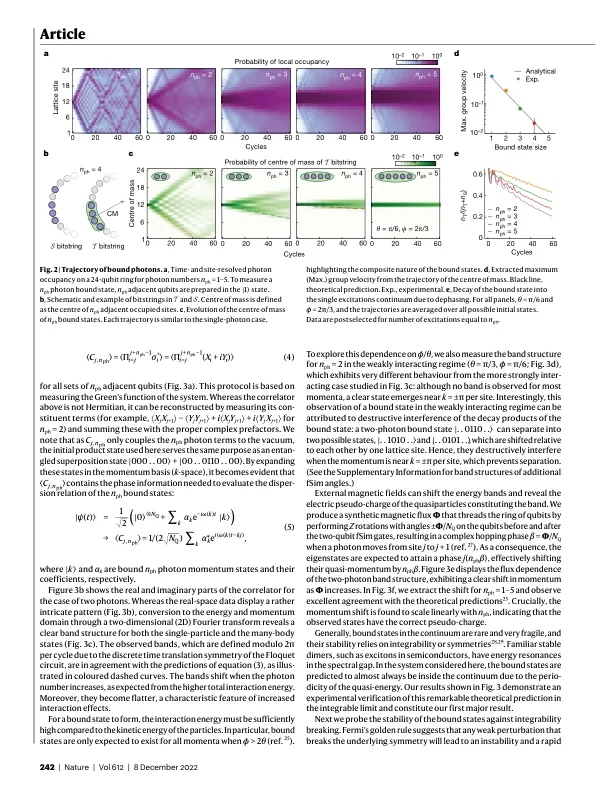
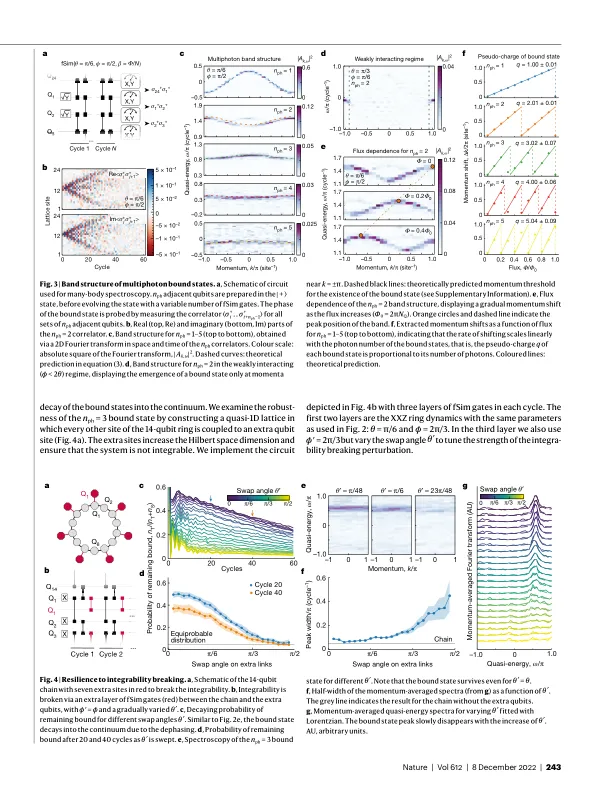
关联粒子系统出现在现代科学的许多领域,代表了自然界中最难解决的计算问题之一。当相互作用变得与其他能量尺度相当时,这些系统中的计算挑战就会出现,这使得每个粒子的状态都依赖于所有其他粒子 1 。三体问题缺乏通解,强关联电子缺乏可接受的理论,这表明当粒子数或相互作用强度增加时,我们对关联系统的理解就会逐渐减弱。相互作用系统的标志之一是多粒子束缚态的形成 2–9 。在这里,我们开发了一个高保真可参数化的 fSim 门,并在一个由 24 个超导量子比特组成的环中实现自旋-½ XXZ 模型的周期量子电路。我们研究这些激发的传播,并观察它们对多达 5 个光子的束缚性质。我们设计了一种相敏方法来构建束缚态的少体谱,并通过引入合成通量来提取它们的伪电荷。通过在环和附加量子位之间引入相互作用,我们观察到束缚态对可积性破坏的意外恢复力。这一发现与不可积系统中的束缚态在其能量与连续谱重叠时不稳定的想法相悖。我们的工作为相互作用光子的束缚态提供了实验证据,并发现了它们在可积性极限之外的稳定性。
相互作用的微波光子的稳健束缚态的形成
主要关键词