机构名称：
¥ 1.0
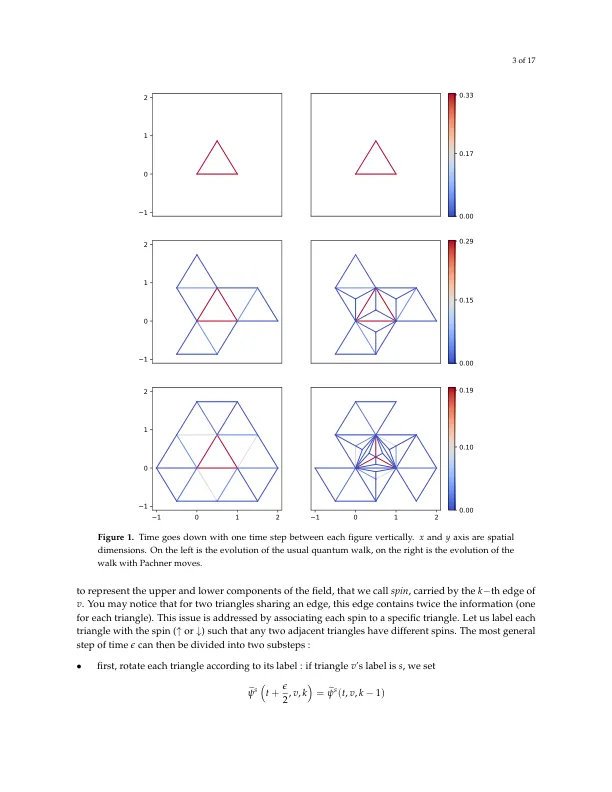
摘要：我们展示了量子细胞自动机的单粒子部分，即量子行走，它位于一个简单的动态三角剖分 2 − 流形上。三角剖分通过 Pachner 移动进行改变，由行走者密度本身引起，从而使表面可以转换为任何拓扑等效的表面。该模型扩展了三角网格上的量子行走，这是作者之一在之前的工作中引入的，其时空极限恢复了 (2+1) 维的狄拉克方程。数值模拟表明，三角形的数量和局部曲率随着 t α e − β t 2 而增加，其中 α 和 β 参数化了几何形状随行走者局部密度变化的方式，并且从长远来看，平坦度会出现。最后，我们还证明了行走者的整体行为在时空随机波动下保持不变。
量子行走引起的动态三角剖分
主要关键词
相关文件推荐
