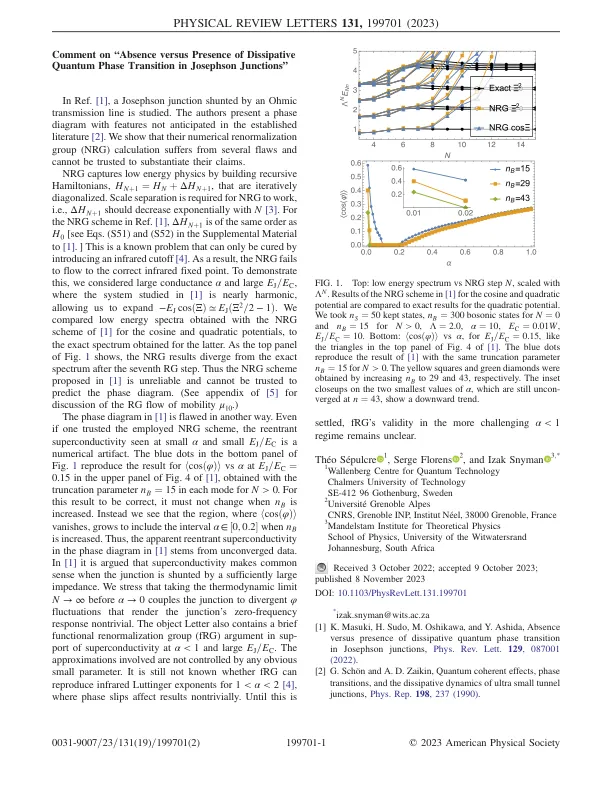
参考。[1],研究了由欧姆传输线拆下的约瑟夫森交界处。作者提出了一个相图,其已建立文献中没有预期的特征[2]。我们表明,他们的数值重归其化组(NRG)计算遭受了几个缺陷,因此无法信任以证实其主张。nrg通过构建递归哈密顿人捕获低能量物理学,hnÞ1¼HnÞΔhnnÞ1,迭代地对角度化。NRG工作需要刻度分离,即,δHnÞ1应用n [3]呈指数降低。参考文献中的NRG方案。[1],δhnÞ1与H 0相同[见等式。(S51)和(S52)在[1]的补充材料中。 ]这是一个已知的问题,只能通过引入红外临界值来治愈[4]。结果,NRG无法流到正确的红外固定点。为了证明这一点,我们考虑了大电导α和大e j = e c,其中[1]中研究的系统几乎是谐波,使我们能够扩展-e j cos- e j cos- ejðejðejðξ2= 2 = 2 - 1Þ。我们比较了余弦和二次电位的NRG方案获得的低能光谱与后者获得的精确光谱。作为图。1显示,NRG的结果与第七个RG步骤后的精确频谱不同。因此,[1]中提出的NRG方案是不可靠的,不能信任预测相图。(有关迁移率μ10的RG流程的讨论,请参见[5]的附录。)[1]中的相图以另一种方式存在缺陷。直到这是即使一个人信任所采用的NRG方案,在小α和小E J = E C处看到的返回超导性是数值伪像。图1在E J = EC¼0时重现Hcosðφivsα的结果。15在图。4,在n> 0的每个模式下以截断参数nb¼15获得。为了正确的结果,当n b增加时,它不得改变。相反,我们看到hcosðφi消失的区域成长为包括间隔α∈½0; 0。2当N B增加时。因此,[1]中相图中的显而易见的重输入超导性源于未交配的数据。在[1]中,有人认为,当连接被足够大的阻抗分流时,超导性是很常见的。我们强调的是,在α→0之前服用热力学极限n→∞,将连接与发散的φ波动相结合,从而使连接处的零频率响应不繁琐。该对象字母还包含一个简短的功能重新归一化组(FRG)参数,在α<1处的超导率和大e j = e c。所涉及的近似值不受任何明显的小参数控制。仍然不知道FRG是否可以以1 <α<2 [4]重现红外Luttinger指数,其中相位滑动在非琐事上影响结果。
物理评论信131,199701(2023)
主要关键词