机构名称:
¥ 1.0
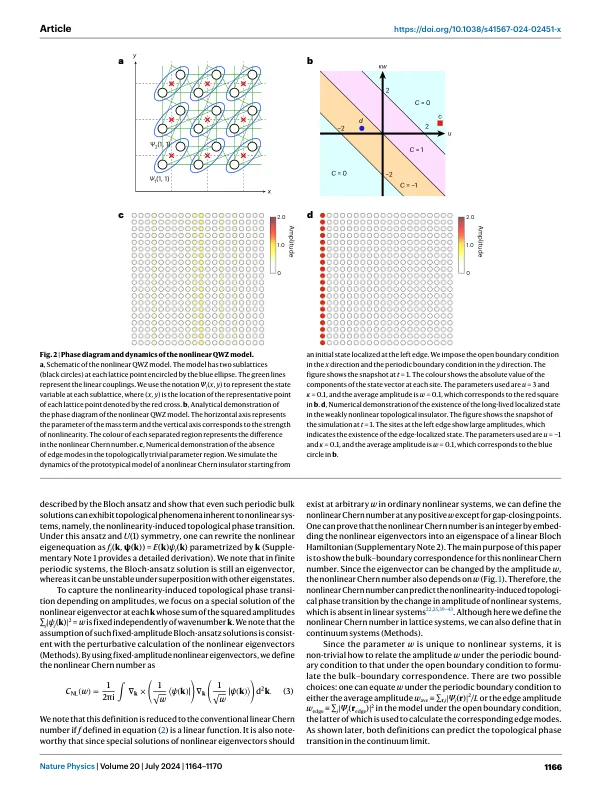
首先通过Chern数字表征量子霍尔效应的表征,拓扑提供了指导原理,以实现对疾病的存在免疫的浓缩含量系统的强大特性。散装对应关系保证了拓扑系统中无间隙边界模式的出现,该模式在拓扑系统中表现出非零的拓扑不变性。尽管最近的一些研究表明,拓扑结构可能会扩展到非线性系统,但尚未了解拓扑不变的非线性对应物。在这里,我们提出了基于二维系统中非线性特征值问题的Chern数字的非线性扩展,并显示了超出弱非线性方案以外的散装 - 边界对应关系的存在。具体而言,我们发现非线性诱导的拓扑相变,其中拓扑边缘模式的存在取决于振荡模式的幅度。我们提出和分析了非线性Chern绝缘子的最小模型,该模型在分析上获得了确切的体积溶液。该模型表现出非线性Chern数的幅度依赖性,为此我们确认了块状 - 边界对应关系的非线性扩展。因此,我们的结果揭示了真正非线性拓扑阶段的存在,这些阶段与线性状态脱节。
非线性诱导的拓扑相变为非线性Chern数
主要关键词