机构名称:
¥ 1.0
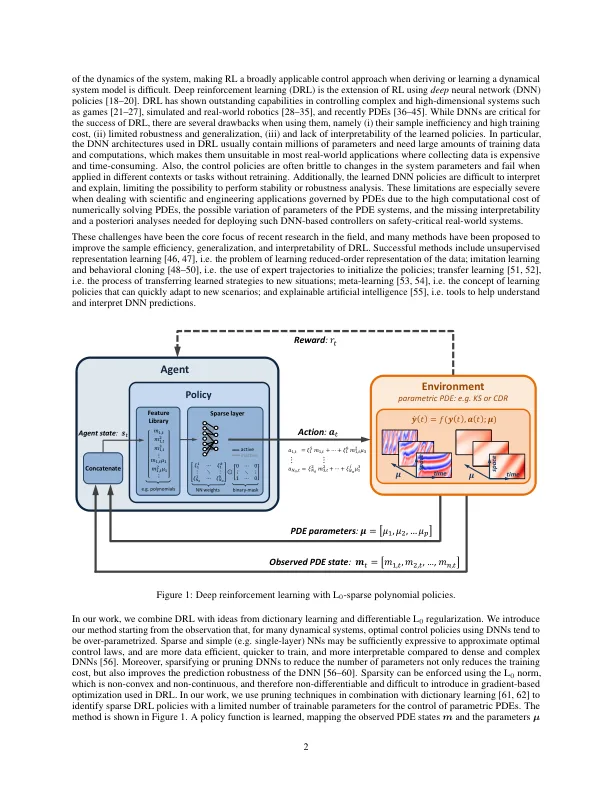
参数偏微分方程 (PDE) 的最优控制在工程和科学领域的许多应用中都至关重要。近年来,科学机器学习的进步为参数偏微分方程的控制开辟了新的领域。特别是,深度强化学习 (DRL) 有可能在各种应用中解决高维和复杂的控制问题。大多数 DRL 方法依赖于深度神经网络 (DNN) 控制策略。然而,对于许多动态系统,基于 DNN 的控制策略往往过度参数化,这意味着它们需要大量的训练数据、表现出有限的鲁棒性并且缺乏可解释性。在这项工作中,我们利用字典学习和可微分 L 0 正则化来学习参数偏微分方程的稀疏、鲁棒和可解释的控制策略。我们的稀疏策略架构与 DRL 方法无关,可以在不同的策略梯度和参与者-评论家 DRL 算法中使用,而无需改变其策略优化程序。我们在控制参数化 Kuramoto-Sivashinsky 和对流-扩散-反应 PDE 的挑战性任务上测试了我们的方法。我们表明,我们的方法 (1) 优于基于 DNN 的基准 DRL 策略,(2) 允许推导所学最优控制律的可解释方程,以及 (3) 推广到 PDE 的未知参数而无需重新训练策略。
具有深度强化学习的参数 PDE 控制......
主要关键词