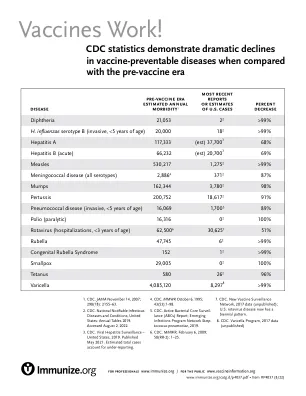
机构名称:
¥ 1.0
我们为估计n个节点M边缘无向膨胀的有效电阻的问题提供了新的算法和条件硬度。我们提供了一个r o o p m✏´1 q - 时间算法,该算法具有很高的可能性,一个r o o o pn✏´1 q-可以估计任何一对节点之间的有效抗性,从而在r o p 1 q -time中估计p 1 q -q mymultiplicative精度。因此,我们获得了一个r o p m✏´1 q - 时间算法,用于估计此类图中所有边缘的有效电阻,从而在先前快速的RO o p m✏´3 {2 Q [Chu等人的最快运行时间上改进(对于稀疏图)。al。2018]和r o p n 2 ✏´1 Q [Jambulapati,Sidford 2018],用于一般图表,而R o P M”n✏2Q用于扩展器[Li,Sachdeva 2022]。我们通过显示有条件的下限来补充这一结果,即一组广泛的算法来计算所有对节点之间的有效电阻的估计值,需要r r⌦p n 2✏´1 {2 q-时间,改善了先前的最佳下限R r 2 p n 2 Q p n 2 p n 2 Q✏usco et usco等。al。2017]。此外,我们利用这些结果基础的工具来获得改进的算法和条件硬度,以勾勒出正面半限定矩阵的伪内的更一般问题,并估计其特征值的功能。
达到最佳有效抗性估计
主要关键词