机构名称:
¥ 1.0
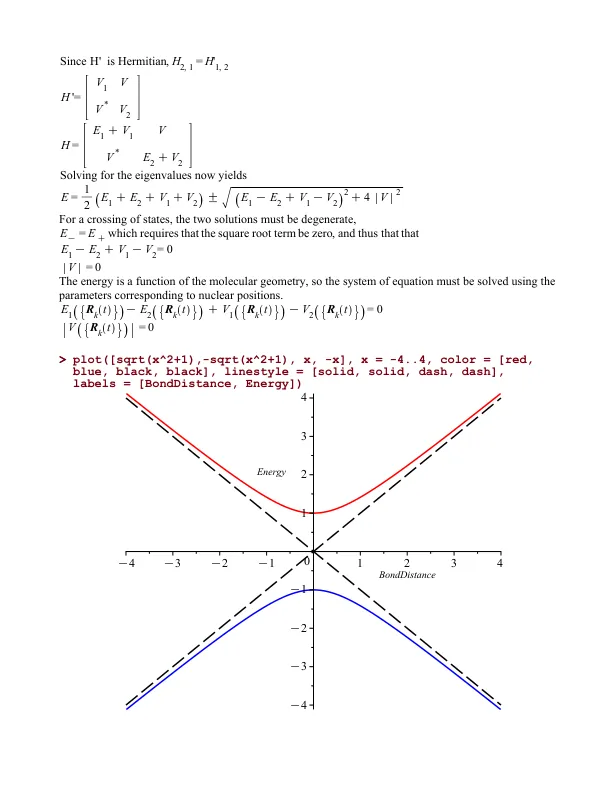
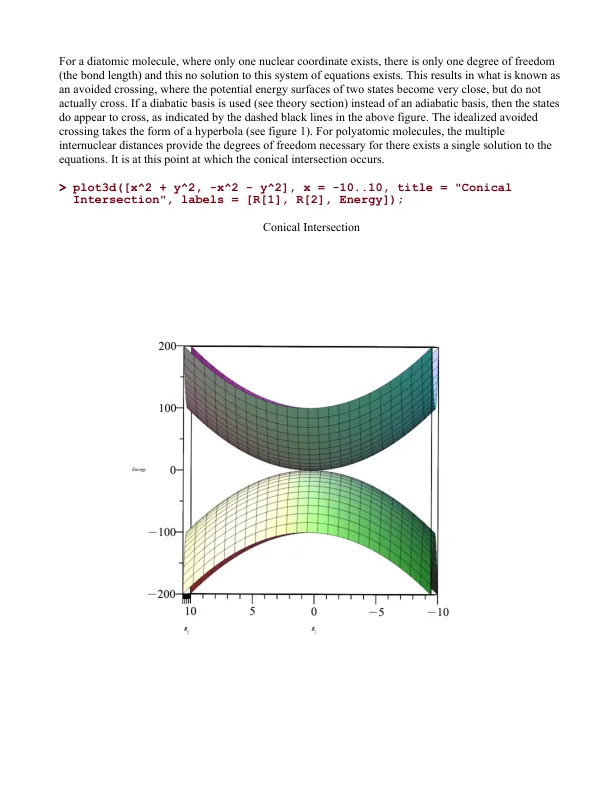
Born-Oppenheimer近似是多体Schrodinger方程的最重要简化之一。通过忽略核运动,可以在所谓的绝热系统中分离核运动和电子运动。在这种绝热状态下,核运动逐渐发生,使该系统始终是瞬时哈密顿量的能量特征功能。Born-Oppenheimer近似导致电子,旋转和振动自由度的典型范式,可以独立计算。当核运动与电子运动耦合时,出现了Oppenheimer制度的局限性,这就是所谓的振动耦合。这种绝热状态通常发生在光化学或化学反应中,在光化学或化学反应中,核运动变得足够重要,可以发挥振动耦合。对于每个绝热状态,可以绘制势能表面(PE)。如下图所示,不同的激发状态势能表面通常在单个点上退化,该点形成了两个表面相交的锥形形状。这是圆锥形的交叉点,即可能的堕落度的0尺寸空间。圆锥形交叉点是理解状态之间的过渡的关键,尤其是在诸如光化学中发生的激发态动力学中。例如,在荧光中,从单重击状态s 1到单线基态S 0发生过渡,这可能是作为圆锥形相交的接缝的过渡而发生的。
动力学和光谱学中的圆锥形交集
主要关键词