机构名称:
¥ 1.0
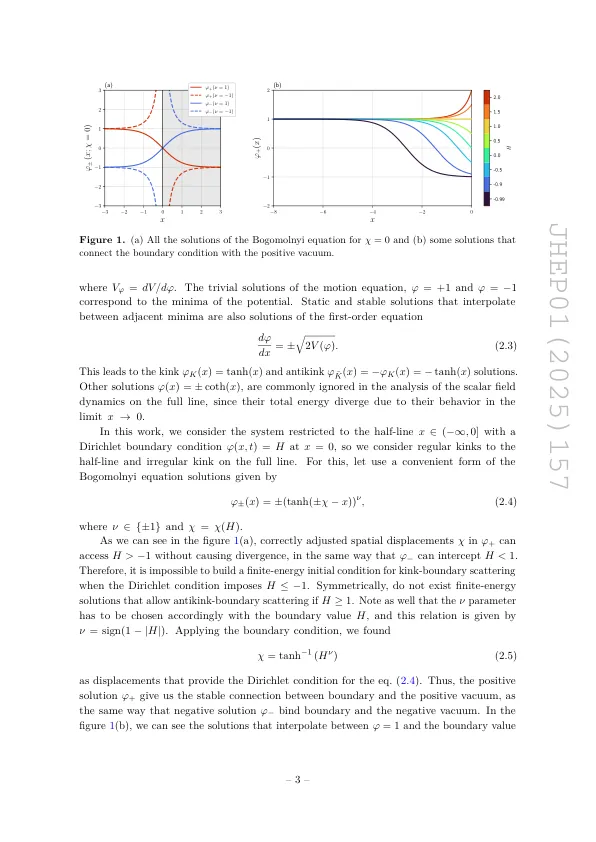
摘要:在这项工作中,我们研究了不整合ϕ 4模型中标量场的动力学,仅限于半线。在这里,我们考虑了单数解,该解决方案插入了dirichlet边界条件ϕ(x = 0,t)= h,并用常规的扭结溶液散射。The simulations reveal a rich variety of phenomena in the field dynamics, such as the formation of a kink-antikink pair, the generation of oscillons by the boundary perturbations, and the interaction between these objects and the boundary, which causes the emergence of boundary-induced resonant scatterings (for example, oscillon-boundary bound states and kink generation by oscillon-boundary collision) founded into complex fractal structures.线性扰动分析用于解释散射过程的某些方面。我们检测到边界附近的两个形状模式。固定点处标量场的功率频谱密度导致几个频率峰。大多数可以用一些有趣的见解来解释散射产品与边界之间的相互作用。
JHEP01(2025)157
主要关键词