机构名称:
¥ 1.0
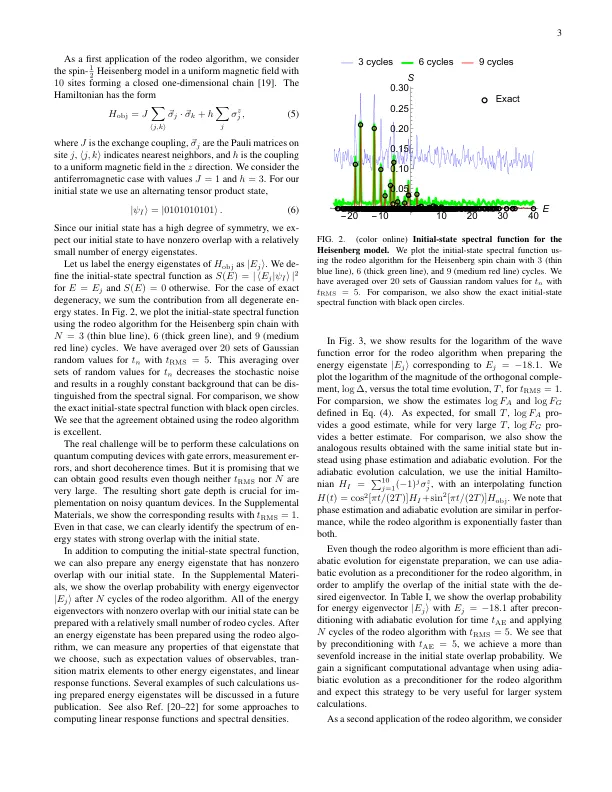
我们提出了一种随机量子计算算法,该算法可以在选定的能量区间 [ E − ϵ, E + ϵ ] 内准备量子哈密顿量的任意特征向量。为了将所有其他特征向量的谱权重降低一个抑制因子 δ ,所需的计算工作量为 O [ | log δ | / ( pϵ )] ,其中 p 是初始状态与目标特征向量的平方重叠。这种方法被我们称为 rodeo 算法,它使用辅助量子位来控制哈密顿量减去某个可调参数 E 的时间演化。对于每个辅助量子位测量,特征向量的振幅都会乘以一个随机因子,该因子取决于它们的能量与 E 的接近程度。通过这种方式,我们以测量次数的指数精度收敛到目标特征向量。除了准备特征向量外,该方法还可以计算哈密顿量的全谱。我们用几个例子来说明其性能。对于误差为ϵ 的能量特征值确定,计算规模为 O [(log ϵ ) 2 / ( pϵ )] 。对于特征态准备,计算规模为 O (log ∆ /p ) ,其中 ∆ 是残差向量正交分量的大小。特征态准备的速度比相位估计或绝热演化的速度快得多。
量子计算的 Rodeo 算法
主要关键词