机构名称:
¥ 1.0
量子色动力学 (QCD) 在从核力将原子核结合在一起到非弹性强子碰撞以及极端条件下物质的行为(如超新星和早期宇宙)等一系列现象中发挥着重要作用。自 20 世纪 70 年代发现以来,已经开发出许多分析和数值工具来研究 QCD。最成功的数值计算方法之一是格点 QCD [1,2]。已经使用格点 QCD 对强子谱 [3 – 5];电弱矩阵元 [6 – 14];高温低密度系统和一些多强子系统 [15 – 18] 的性质进行了高精度计算(最近的综述见参考文献 [19,20])。然而,一些重要可观测量的格点 QCD 计算受到所用随机采样中存在的符号问题的限制。例如,模拟高密度的 QCD [21-25]、与超新星和早期宇宙相关的 QCD,或者带有 θ 项的 QCD,存在符号问题 [26],超出了经典计算机的大规模能力范围。20 世纪 80 年代,费曼 [27] 和贝尼奥夫 [28] 认识到了经典计算机模拟量子物理的局限性,他们提出使用受控量子系统来模拟感兴趣的量子系统。最近,实验室中对量子系统的控制迅速改进,导致了最初几代量子计算机的诞生。人们已经探索了许多不同的平台,包括但不限于:
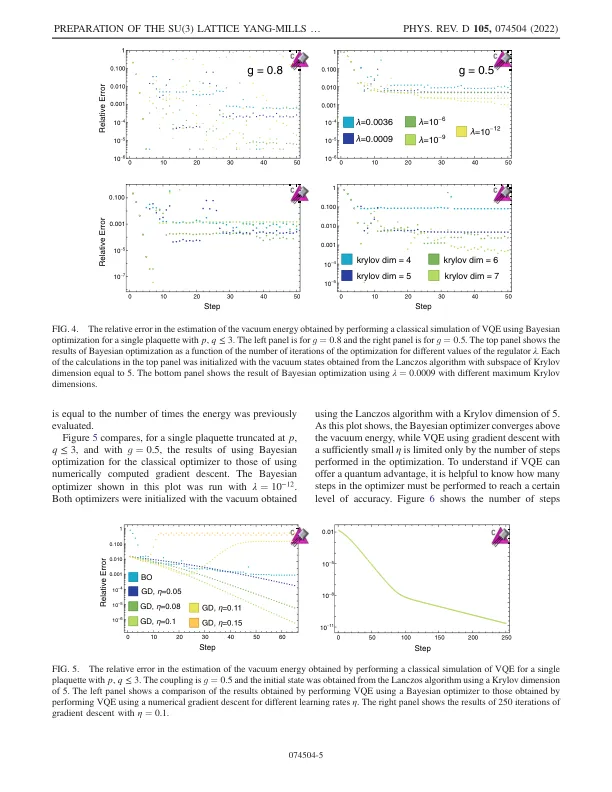
用变分量子方法制备 SU(3) 格子杨-米尔斯真空
主要关键词