机构名称：
¥ 1.0
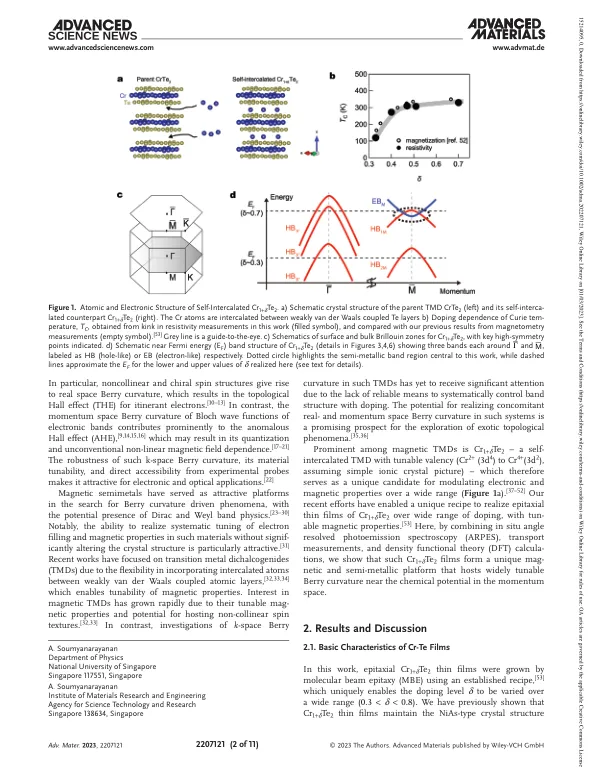
近年来，人们发现了由电子自旋自由度与新出现的几何和拓扑效应相互作用而产生的令人着迷的新型凝聚态现象。[1,2] 其中最突出的是贝里曲率 Ω 的概念，它源于电子波包穿过闭合环路时积累的几何相。[3,4] 在晶体固体中，这种贝里曲率可以解释为作用于运动电子的有效磁场，因此在霍尔输运实验中表现突出。[1] 例如，其积分在动量空间的量化，一种称为能带拓扑的现象，导致量化电荷和自旋霍尔效应。[5–8] 另一方面，磁性材料表现出丰富的实空间和动量空间贝里曲率表现。[9,10]
Fujisawa - 磁场中可广泛调节的贝里曲率......
主要关键词
相关文件推荐
![]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]，3 月 11 日星期二......](/simg/3/3bce187fc3200455d5aba0e68e59e409af199c11.webp)
