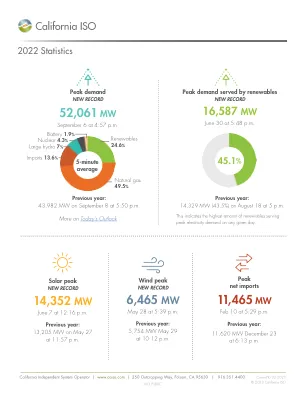
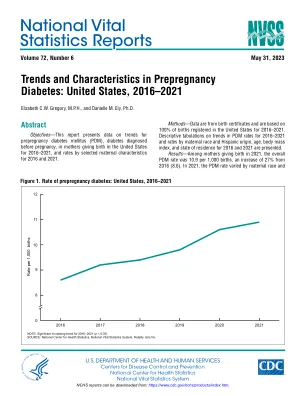
机构名称:
¥ 1.0
摘要:本文提出了一种新型的监督学习方法——统计自适应傅里叶分解(SAFD)。SAFD 使用正交有理系统或 Takenaka-Malmquist(TM)系统为训练集建立学习模型,在此基础上可以对未知数据进行预测。该方法侧重于信号或时间序列的分类。AFD 是一种新开发的信号分析方法,它可以自适应地将不同的信号分解为不同的 TM 系统,引入了傅里叶类型但非线性和非负的时频表示。SAFD 将学习过程与 AFD 的适应性特征充分结合起来,其中少量的学习原子足以捕获信号的结构和特征以进行分类。SAFD 有三个优点。首先,在学习过程中会自动检测和提取特征。其次,所有参数都由算法自动选择。最后,将学习到的特征以数学形式表示出来,并可以根据感应瞬时频率进一步研究特征。通过心电图 (ECG) 信号分类验证了所提方法的有效性。实验表明,该方法比其他基于特征的学习方法效果更好。
统计自适应傅里叶分解 (SAFD)
主要关键词