机构名称：
¥ 2.0
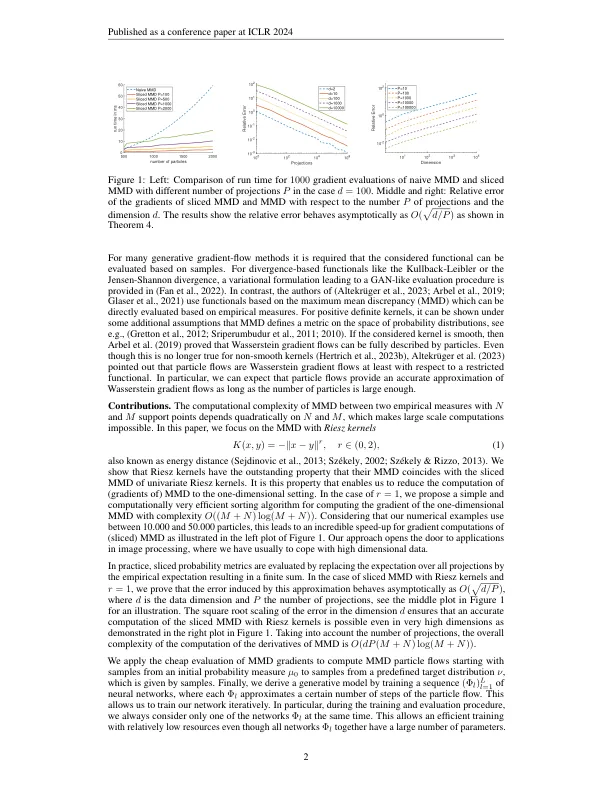
最大平均差异（MMD）流在大规模计算中遭受高计算成本的影响。在本文中，我们表明MMD用Riesz内核K（x，y）= −∥ x -y∥r，r∈（0，2）具有出色的属性，可以有效地计算。我们证明，Riesz内核的MMD（也称为Energy距离）与其切片版本的MMD相吻合。因此，可以在一维设置中执行MMD梯度的计算。在此，对于r = 1，可以应用一种简单的排序算法，以减少O（Mn + N 2）到O（（M + N）log（M + N））的复杂性，以使用M和N支持点进行两个测量。作为另一个有趣的后续结果，可以通过Wasserstein-1距离从上和下估算紧凑型措施的MMD。对于实现，我们仅使用有限的切片p，近似切片MMD的梯度。我们表明结果误差具有复杂性o（p
用riesz内核切成薄片的MMD流量
主要关键词
相关文件推荐
