机构名称:
¥ 1.0
硬币赋予的自由度,如 [3, 9] 所述。这与所谓的离散时间 QW 形成对比,在离散时间 QW 中,额外的硬币自由度会定期翻转 [3]。我们特意保留这种命名法,以便与 QW 社区建立联系。这也是合理的,因为周期性驱动的 Floquet 问题 [10] 的物理实现仍然会随时间不断演变,例如参见下面等式 (1) 中的 QKR 哈密顿量。我们现在利用 AOKR 实验的多功能性来实现基于这种 CTQW 的量子搜索协议。但我们的主要目标不是提高高度专业的计算机科学算法的性能,而是提出一种方法,通过该方法可以使用玻色-爱因斯坦凝聚态 (BEC) 的标准实验在由 BEC 形成的一维离散动量态网格基组内进行简单的量子搜索。该基础由周期性势能定义,该势能以双光子反冲为单位,以离散步骤改变 BEC 的动量。本文结构如下:第 2 部分,在简要介绍量子共振条件下 AOKR 的时间演化之后,我们介绍了适用于我们实验系统的搜索协议。因此,我们提出了两种不同的技术,以通过测量特定演化后的动量分布来获得所需状态。在第 3 部分,我们讨论了搜索协议的时间缩放,最后对用于搜索的 CTQW 的实现的重复性和命中时间进行了一般性评论。第 4 部分总结了本文。
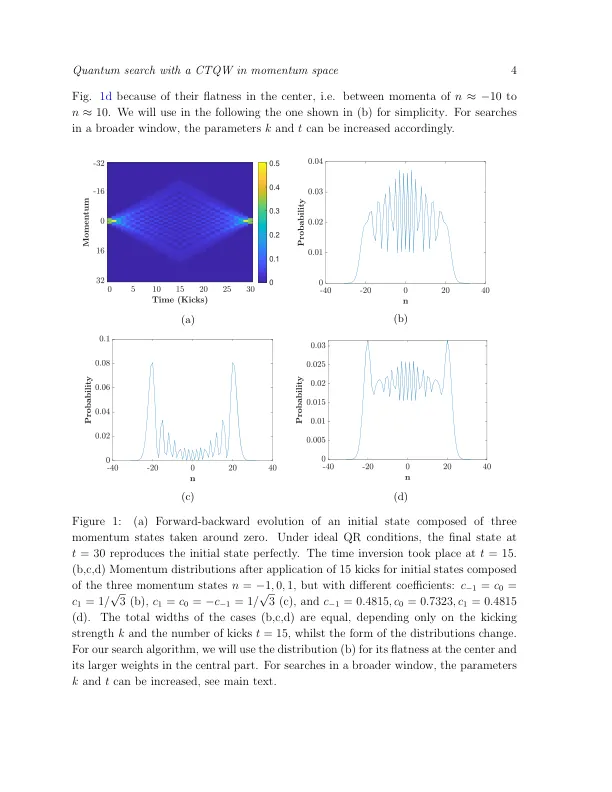
动量空间中连续时间量子行走的量子搜索
主要关键词